面向图像的秘密共享算法设计
门限秘密共享
现在应用广泛的的秘密共享主要框架即门限秘密共享
门限秘密共享的工作原理如下:
- 秘密分割:首先,一个秘密信息被分割成多个部分,通常是通过一些数学算法进行划分。这些部分称为“份额”(shares)或“部分秘密”(partial secrets)。
- 门限条件:定义一个门限值(threshold),只有在满足门限值要求的份额数量或者特定的份额组合之下,才能还原出原始的秘密信息。这个门限值可以是任何数字,通常是一个预先确定的整数。
- 分发份额:将这些份额分发给不同的参与者,每个参与者只持有其中的一部分份额,而且不知道其他参与者持有的份额内容。
- 重构秘密:当需要还原秘密信息时,至少要达到门限值数量的参与者合作,将他们的份额组合在一起,才能成功还原出原始的秘密。
比较常见的门限秘密共享方案基本都是基于数学问题
Shamir秘密共享方案
Shamir密码共享方案建立在一条数学定理上:
n次平面代数曲线(一次时为直线),至少需要知道该曲线上的n+1个点的坐标

当需要恢复秘密时,我们需要用到拉格朗日插值公式
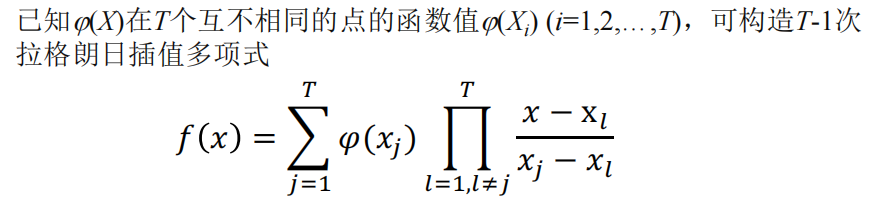
基于中国剩余定理的秘密共享
顾名思义,该方案是基于中国剩余定理
中国剩余定理(CRT)是数论中的一个定理,描述了一组线性同余方程的解的存在性和唯一性。具体来说,如果有一组两两互质的正整数$ n_1, n_2, …, n_k $,以及任意整数$ a_1, a_2, …, a_k $,则下面的一组同余方程:
存在一个唯一解$ x $,在模$N = n_1n_2…n_k $的意义下唯一。CRT提供了一种算法来找到这个唯一解。
基于CRT的秘密共享步骤如下:
选择互质的模数:
选取$ k $个大的、两两互质的正整数$ n_1, n_2, …, n_k $,它们的乘积要大于秘密数$ S $。分配秘密:
对于秘密$ S $,选择$ k $个整数$ a_1, a_2, …, a_k $,使得$ a_i \equiv S \pmod{n_i} $。这里每个$ a_i $就是秘密的一个“份额”。分发份额:
将每个$ a_i $和对应的模数$ n_i $作为一个份额,分发给参与者。每个参与者只能得到一个$ a_i $和$ n_i $。秘密恢复:
当需要恢复秘密$ S $时,收集足够数量的份额$ (a_i, n_i) $对。只要收集到的份额数目大于或等于原来分割的份额数目,就可以利用CRT计算出原始的秘密$ S $。利用CRT计算原秘密:
为了恢复秘密,首先计算所有模数的乘积$ N = n_1n_2…n_k $。然后,对于每个份额$ (a_i, n_i) $,计算$ N_i = N / n_i $和$ N_i $的模$ n_i $逆元$ m_i $,即$ m_iN_i \equiv 1 \pmod{n_i} $。最后,利用下面的公式计算$ x $:这个$ x $在模$ N $下等同于原始的秘密$ S $。
Brickell秘密共享
该方案是Shamir秘密共享方案的推广,由一维方程转向多维向量


面向图像的秘密共享
事实上,当我们需要对图像类型的信息进行秘密共享时,针对字符数据的秘密共享方案依然能够很好的工作
因为图像的每个像素点都可以由RGB表示(灰度图为一个灰度值),所以我们可以找到合适的方案对色值进行加密并共享,只需在原先的秘密共享方案上增加一些预处理和后处理的过程
预处理即将图像特征提取,转化为二进制数据
而后处理则是将解密后的二进制数据转回图像
而密文数据的中间传输形态同样也可以是图像,虽然看起来是一些杂乱无章的噪点
算法选择
基本的算法框架我们选用Shamir秘密共享方案
相比于CRT中进行的幂运算,Shamir中涉及的多项式运算更适合同时对整个图像数组进行计算
但是在图像类型的Shamir秘密共享中有一点需要注意:
这里的模数q需要选取一个素数,而我们保存的影子图像的每个通道位深只有8位,即0到255
如果我们选择的模数q如果小于255,那么一些像素点算出来的多项式值的精度便会丢失
而如果我们选择的模数大于255,那么如果像素点的多项式值模257后的余数大于255时,我们无法将其直接作为像素值保存,这部分像素点的数据无法直接传输
所以问题的关键是如何保存由模数造成的无法传输的额外信息
这里我们选择一个与256较为接近的模数,即257,这样我们只需要记录一种情况,即多项式的值mod257后余256
我们考虑将这些余256的某通道像素点在图像数组中的索引放在一个列表中,并将这个列表保存在图片的元数据(Meta data)中
影子图像生成
影子图像生成的步骤如下图:
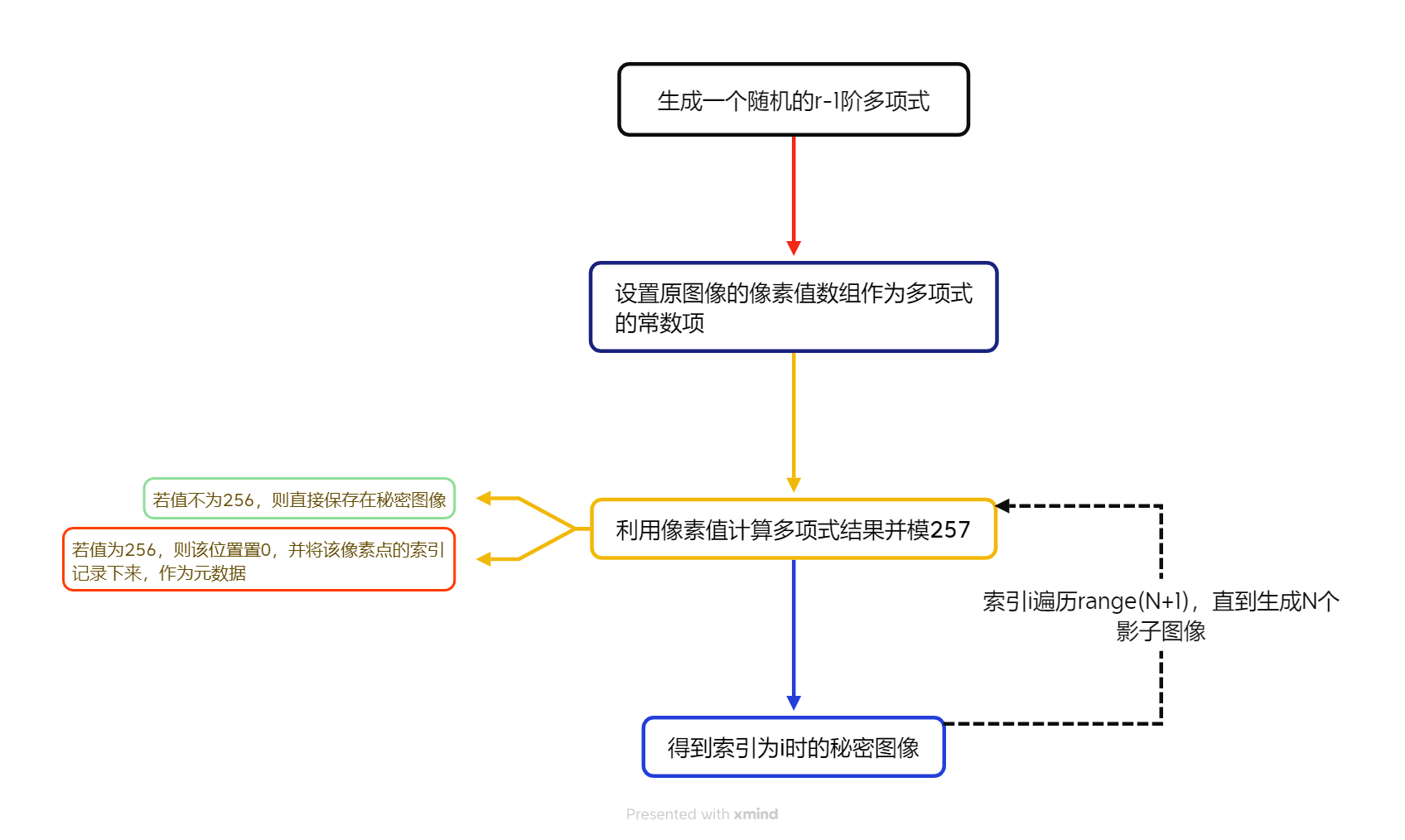
- 随机生成多项式系数,并将原像素值(即秘密)作为$a_0$。
- 将原图像数组碾平,使得三个通道R、G、B上的值可以同时进行多项式计算,并将计算结果合并为彩色的影子图像。
- 如果生成影子图像时,像素点上的值为256,则将其置0,并保存索引信息到元数据中
- 遍历索引,直到生成N个影子图像
原图像恢复
恢复原图像时需要先将元数据中存储的索引数组恢复为一个图像数组,并与秘密图像提取的数组相加,这样就能恢复余数为256的像素点的信息
而恢复算法则选用拉格朗日插值法
原图像恢复的步骤如下图:
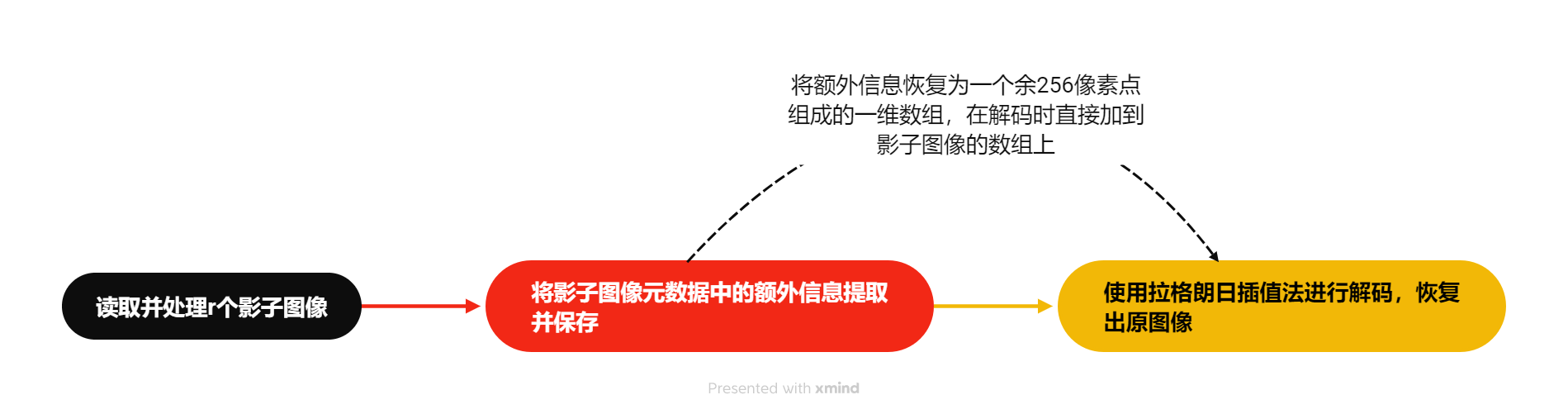
- 读取并处理r个影子图像,每个图像的三通道值碾平为一维数组
- 将影子图像元数据中的额外信息提取并保存,恢复为一个余256像素点组成的一维数组,并直接加到影子图像的数组上
- 每次从r个影子图像数组各读取一个像素值,使用拉格朗日插值法恢复出原图像的一个像素值
创新点
其实一开始我有考虑过将程序改造为多线程,并将其作为一个创新点。但是后来我意识到,秘密共享其实是一个计算密集型的过程。对于python的并发编程来说,I/O密集型的程序比计算密集型的程序更能充分利用多线程的好处。在本任务中使用多线程,对速度的提升不大。
无损恢复
本算法最大的创新点,就是实现了无损的图像秘密共享过程,并且生成的影子图像的大小不会太大
较为常见的模251和模257都会不同程度上地导致原图像信息的丢失
如果我们能将模256的信息额外保存在图片的元数据中,就能实现无损恢复
将中间影子图像的格式选为png,我们能够快速的将额外信息存在文件的chunk中
1 | def insert_text_chunk(src_png, dst_png, text): |
那么选择存入元数据的额外信息需要保证能有很高的信息密度,很显然将余256的索引存在一个数组*是个合适的选择
通过numpy提供的where()方法,我们可以快速的从数组中找到值为256的元素的索引,并利用该索引置0
1 | indices = np.where(secret_img == 256)[0] |
在恢复图像时,我们只需要将影子图像的数组与从额外信息恢复的同尺寸的数组相加即可:
1 | imgs_add = np.zeros_like(imgs,dtype=np.int32) |
一个py文件实现所有功能
而另一个创新点,则是将整个秘密共享过程集成在一个python源码中。在控制台运行该py文件时,通过设置选项和传入不同的参数,我们能够完成三种任务:影子图像生成、原图像恢复以及图像像素值对比
这种一站式的解决方案极大地简化了操作流程,用户无需切换不同的程序或脚本即可完成整个秘密共享的周期。
程序中的关键选项说明如下:
-e/--encode:这个选项后跟原始图像的路径,用于指定需要进行秘密共享加密的图像文件。-d/--decode:这个选项后跟解密后的图像的保存路径,用于指定解密操作的输出目录。-n:这个选项后跟的参数设置了要生成的影子图像的总数,即秘密共享的分片数。-r:这个选项后跟的参数设置了重建原始图像所需的最少影子图像数,即秘密共享的阈值。-i/--index:这个选项接受一个或多个整数参数,代表用于解密操作的影子图像的索引。-c/--compare:这个选项后跟两个图像文件的路径,用于比较这两个图像的差异。
同时,你还可以使用-h参数调出程序的说明书,这些功能都得益于python的argparse库
值得注意的是,解密时影子图像需和Shamir.py存储在同一路径下,并以secret_{index}的规则命名,且格式为PNG
显示直观且详细
通过精心设计的命令行界面,本程序在执行各种操作时,如加密、解密和比较图像,都会给出清晰的进度反馈和详尽的状态信息。例如,在解密过程中,程序不仅会显示当前处理的进度条,还会在完成后输出解密所用的总时间,使用户能够明确地了解到任务执行的效率。
具体实现如下:
进度条显示:在
decode函数中,通过计算当前处理的像素与总像素数的比例,我们实现了一个动态更新的进度条。这个进度条不仅在视觉上给出了解密过程的即时反馈,还通过百分比精确地表达了当前的完成状态。1
2
3
4
5
6
7
8
9percent_done = (i + 1) * 100 // dim
if last_percent_reported != percent_done:
if percent_done % 1 == 0: # 每增加1%更新一次进度
last_percent_reported = percent_done
bar_length = 50
block = int(bar_length * percent_done / 100)
text = "\r[{}{}] {:.2f}%".format("█" * block, " " * (bar_length - block), percent_done)
sys.stdout.write(text)
sys.stdout.flush()文件大小的动态显示:使用
get_file_size函数,程序在保存每个影子图像和恢复的原图像后,都会输出文件的大小。这个大小是动态计算并格式化的,根据文件的实际大小自动选择最合适的单位(如B, KB, MB),使信息展示更为直观。1
2size = get_file_size(secret_img_path)
print(f"{secret_img_path} saved.", size)图像比较的详细报告:在比较两个图像时,
compare_images函数不仅输出了两图像的平均差异值,还输出了最大差异、最小差异以及差异的标准差,为用户提供了全面的图像差异分析。该报告的结果能充分说明本算法在无损秘密共享上的可靠性。1
2
3
4print("Mean difference:", diff_value)
print("Max difference:", round(np.max(diff), 4))
print("Min difference:", round(np.min(diff), 4))
print("Standard deviation of difference:", round(np.std(diff), 4))运行时间的直观显示:在程序的关键节点,如加密结束或解密完成后,程序会计算并显示整个操作所花费的时间。这不仅提供了操作的即时反馈,而且还允许用户对程序的性能进行评估。通过记录操作开始和结束的时间戳,程序可以输出精确到毫秒的运行时间,使得性能测试结果更加准确。
1
2
3
4start_time = time.time() # 操作开始前记录时间
# ... 执行操作 ...
end_time = time.time() # 操作结束后记录时间
print(f"Operation completed. Time elapsed: {end_time - start_time:.2f} seconds.")
以上功能的实现,确保了用户在使用本程序时,能够获得详尽的操作信息,包括操作进度、文件大小以及操作耗时等。这些直观的显示信息不仅提高了用户操作的透明度,也增强了用户对程序性能的信心。
实验结果
在实验中,我会对程序的不同功能的执行效果进行演示,并通过消融实验测试本程序实现的无损模块在各方面上的提升
我会使用我的头像作为测试样本,原图像avatar.png如下

原图像的大小为243KB,尺寸为640*640
之所以选择png格式的原图是因为PNG是一种无损压缩的图像格式,这意味着在重新恢复图像时,像素数据不会发生变化,这更有利于我们精准测试整个过程是不是无损的秘密共享
功能测试
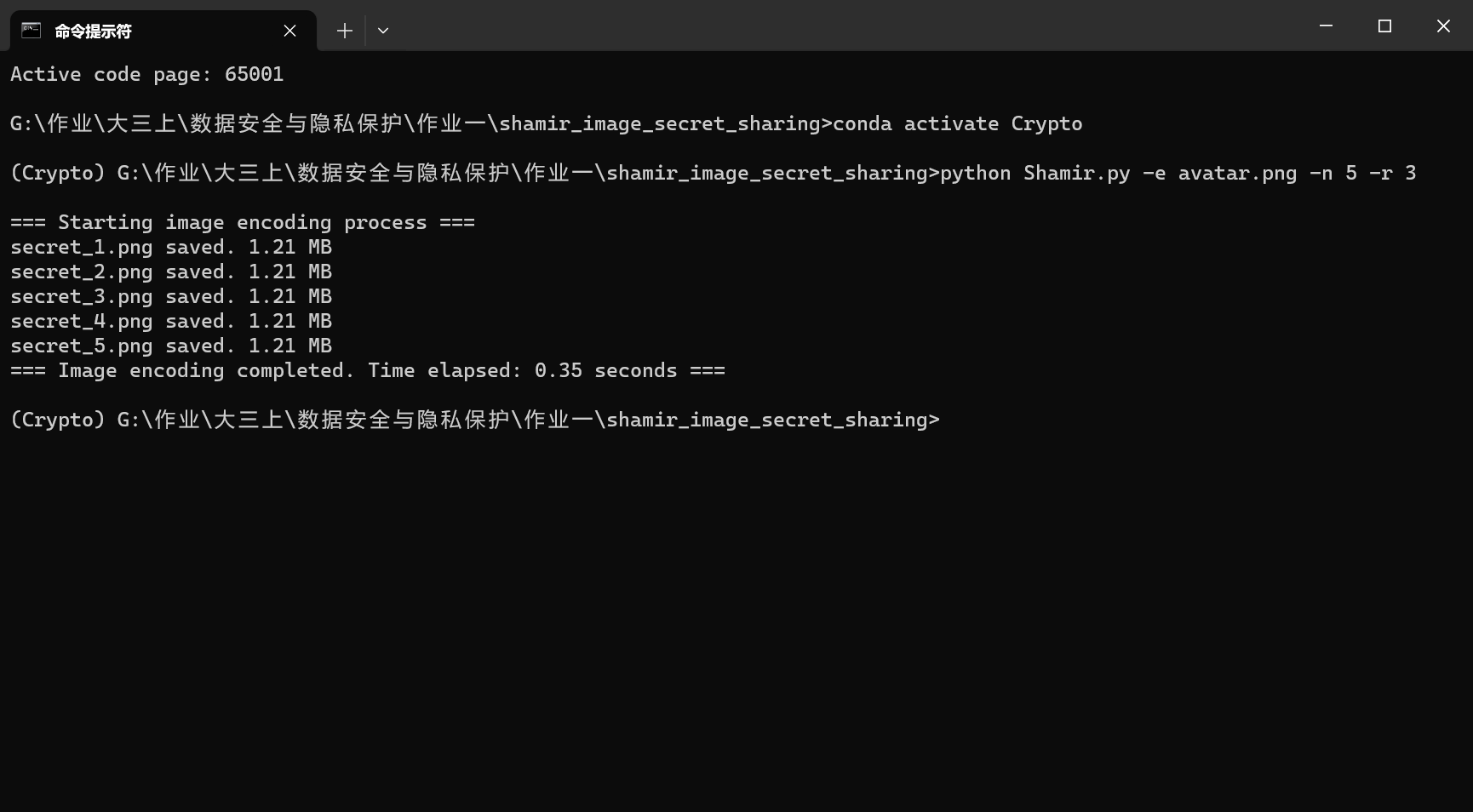
首先进行影子图像的生成,执行如下指令
1 | python Shamir.py -e avatar.png -n 5 -r 3 |
成功生成5张影子图像
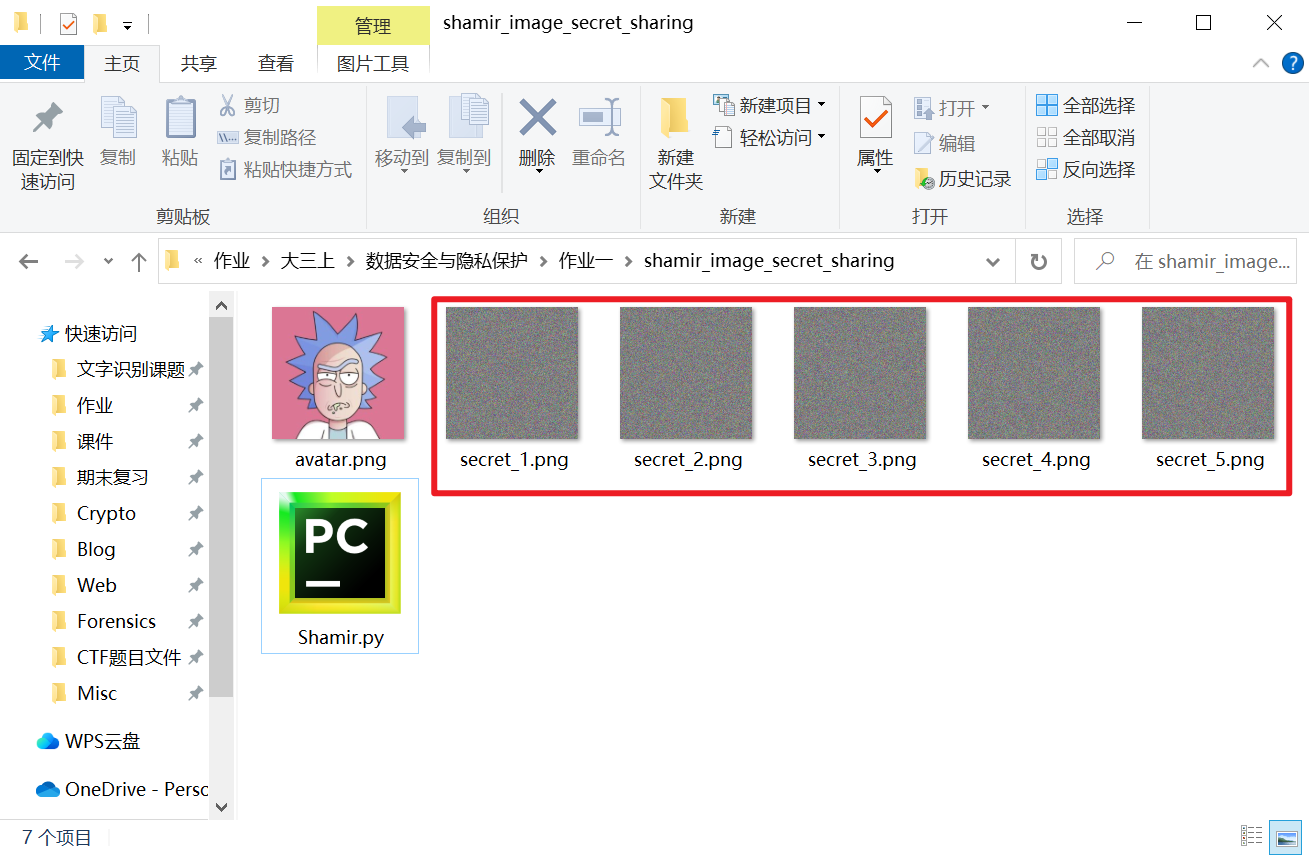
接下来使用图像恢复功能,执行如下指令
1 | python Shamir.py -d avatar_recover.png -r 3 -i 1 4 5 |
我们选用序号为1、4、5的影子图像来恢复原图像
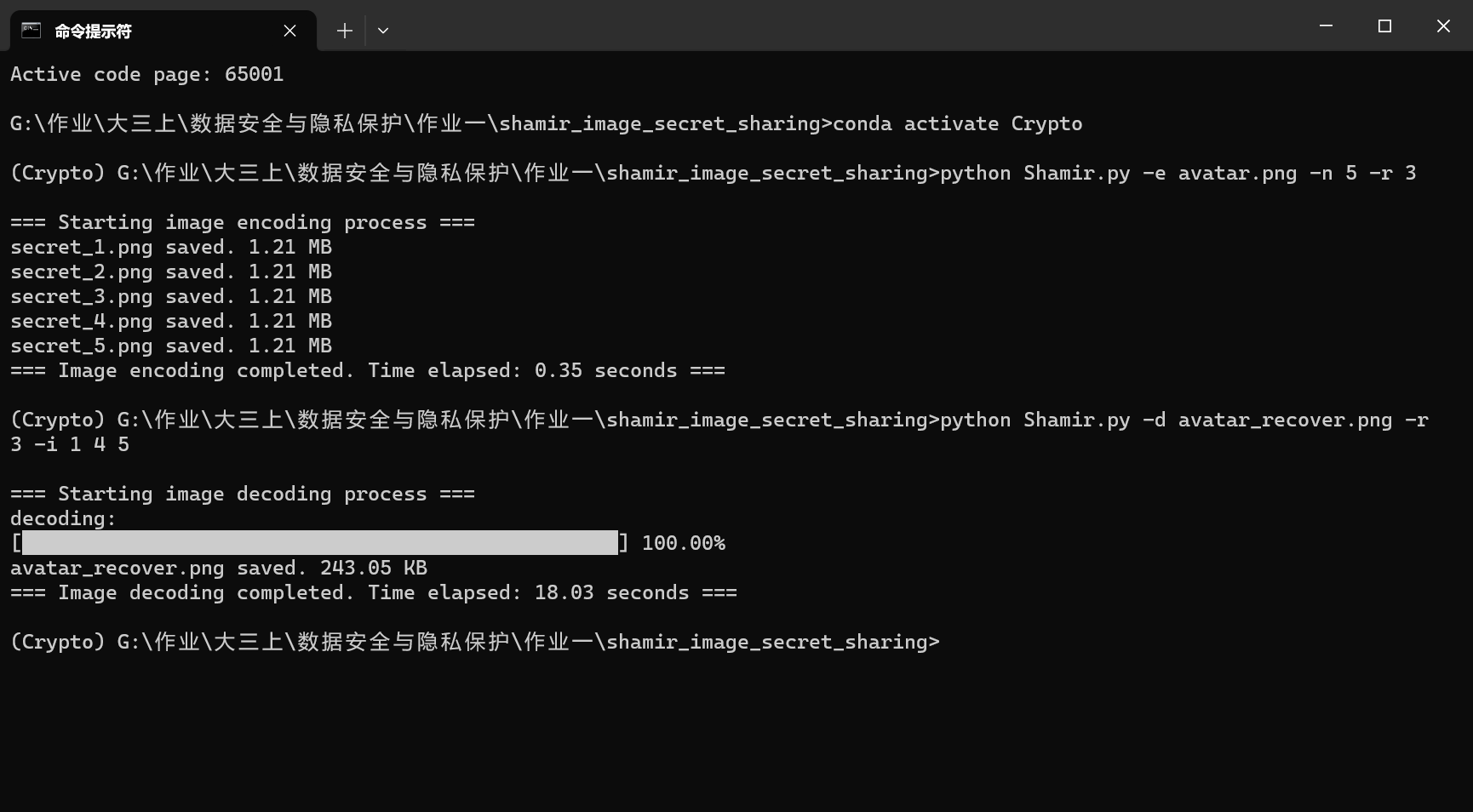
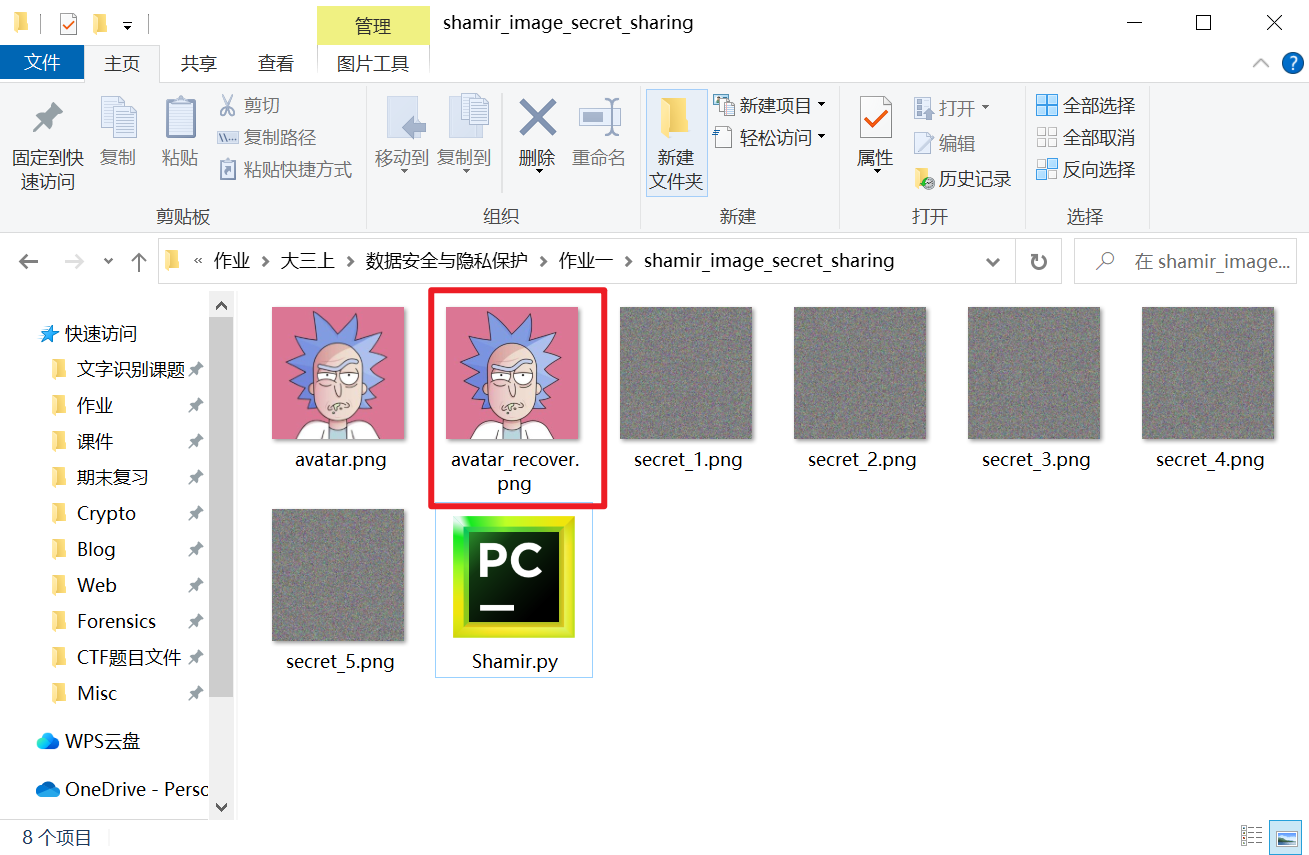
最后我们来对比一下恢复得到的图像与原图像之间像素值的差别
执行如下命令
1 | python Shamir.py -c avatar_recover.png avatar.png |
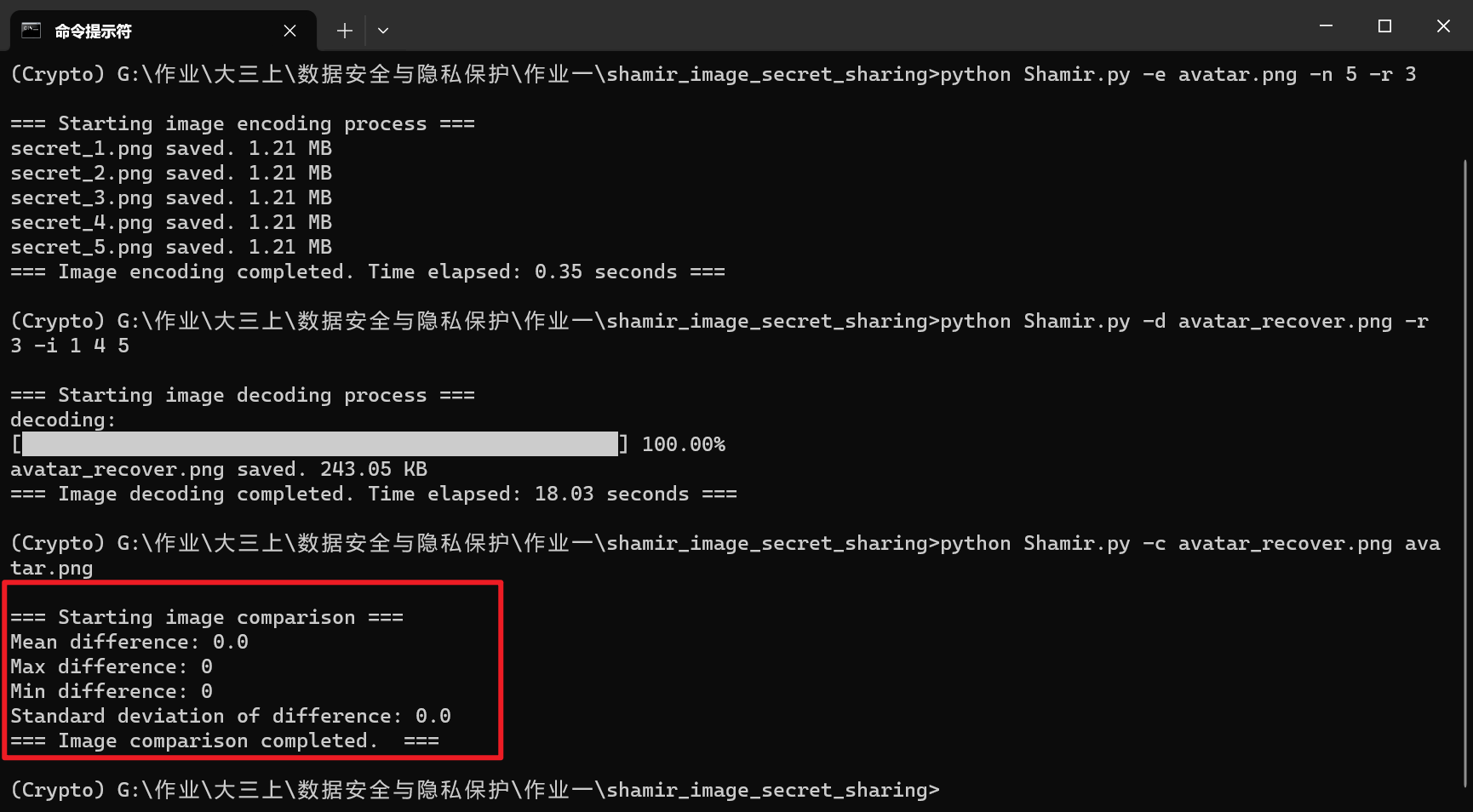
恢复图像与原图像完全一致,说明成功实现了无损的图片秘密共享
如果我们想同时执行所有任务,完成加密解密和对比,可以执行下面这条指令
1 | python Shamir.py -e avatar.png -n 5 -r 3 -d avatar_recover.png -i 1 4 5 -c avatar_recover.png avatar.png |
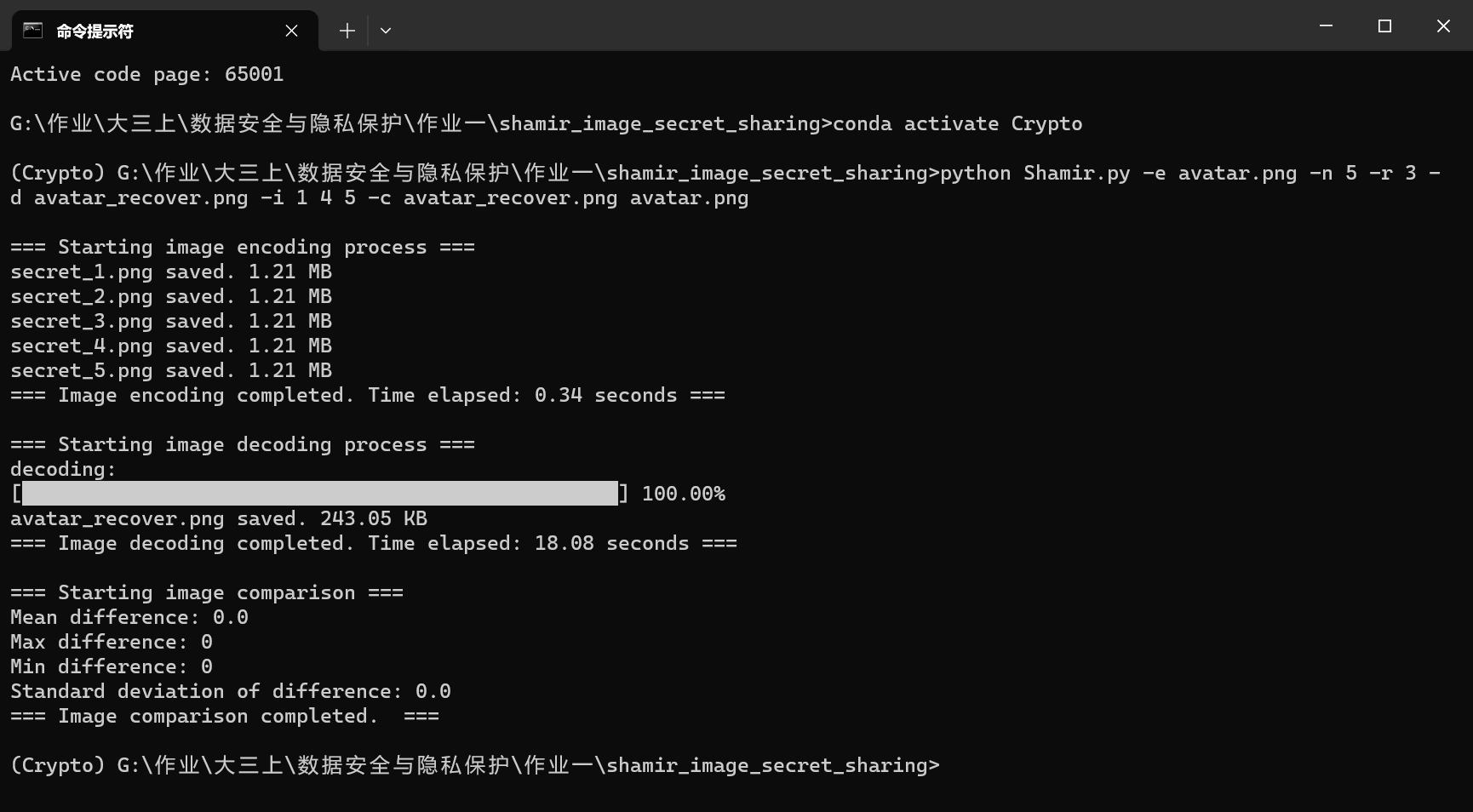
消融实验
在消融实验中,我会测试额外信息这个模块的影响
将源代码中有关extra部分的内容去掉后,我们再次执行整个过程
下图是去掉额外信息模块后的算法运行结果和恢复的图像
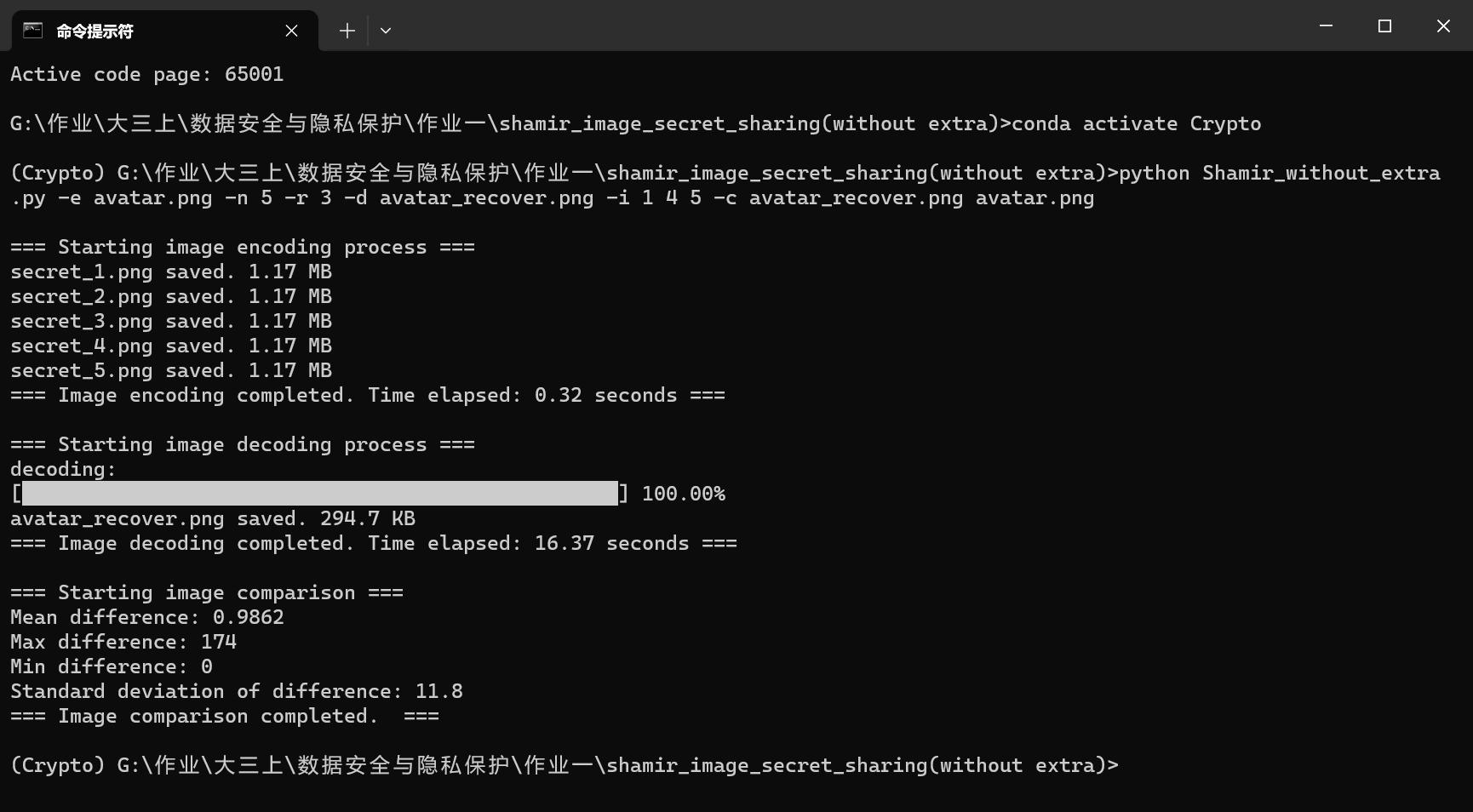
![]()
下图是拥有额外信息模块的算法运行结果和恢复的图像
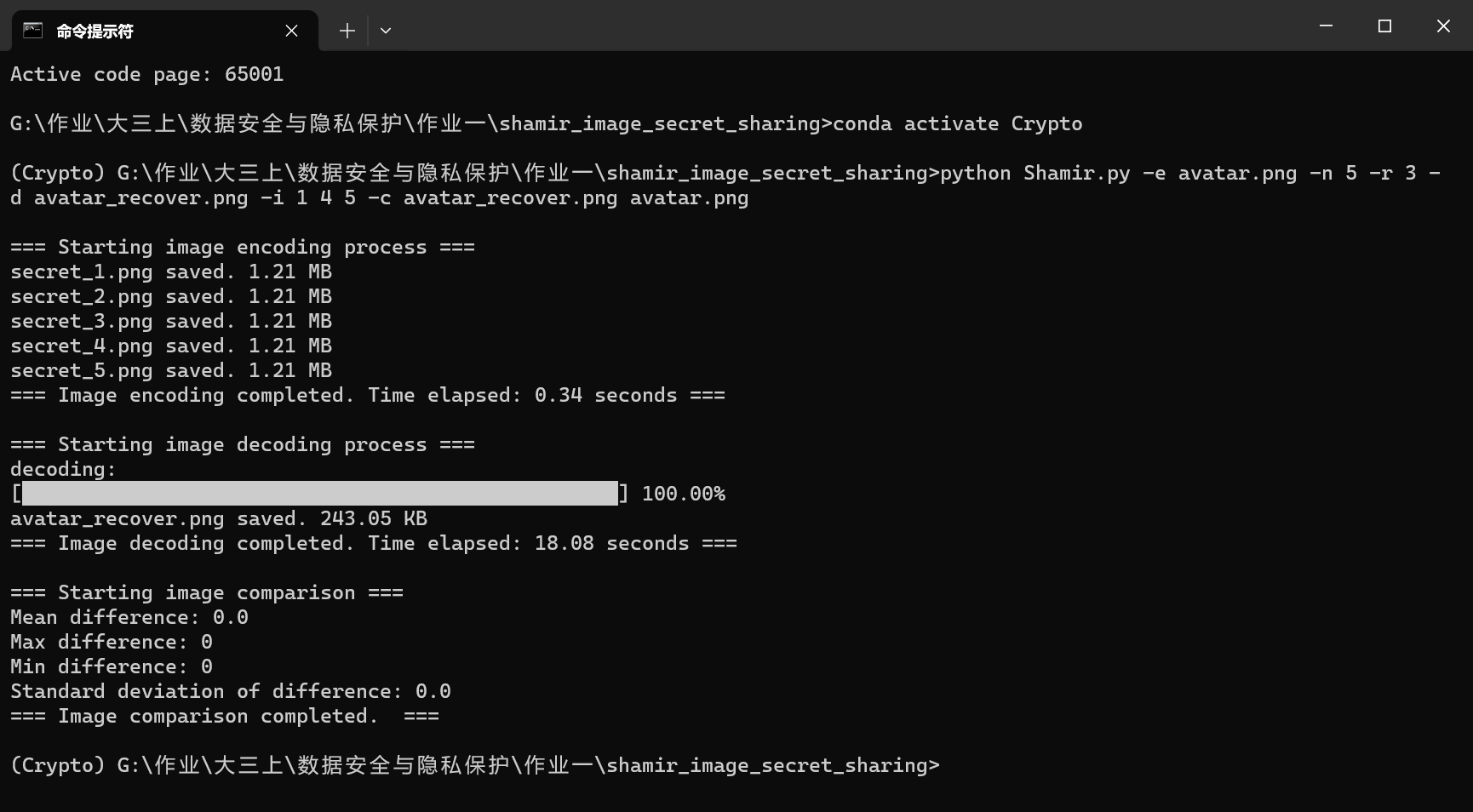
![]()
首先是无损方面,没有额外信息模块的算法因为余256像素点的影响,平均像素值差异为0.9862
而拥有额外信息模块的算法恢复的图片与原图完全一致,平均像素值差异为0
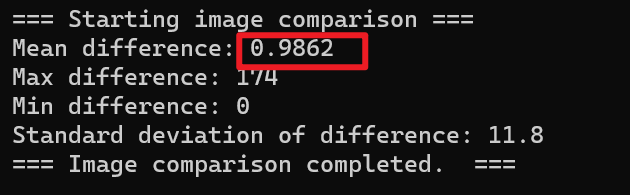
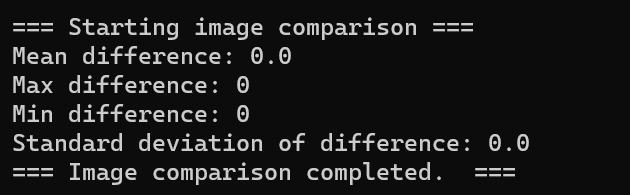
直接观察恢复的图像我们能够更直观的发现原因


没有额外信息模块的算法恢复的图像中,有许多因为丢失信息而恢复失败的像素点
上述差别说明额外信息模块使得信息都被保留,实现了无损秘密共享
除了图像指令,我们还应关注算法的时间以及影子图像的大小
额外信息模块中进行了更多的运算以及存储,我们需要了解其对于用户体验的影响
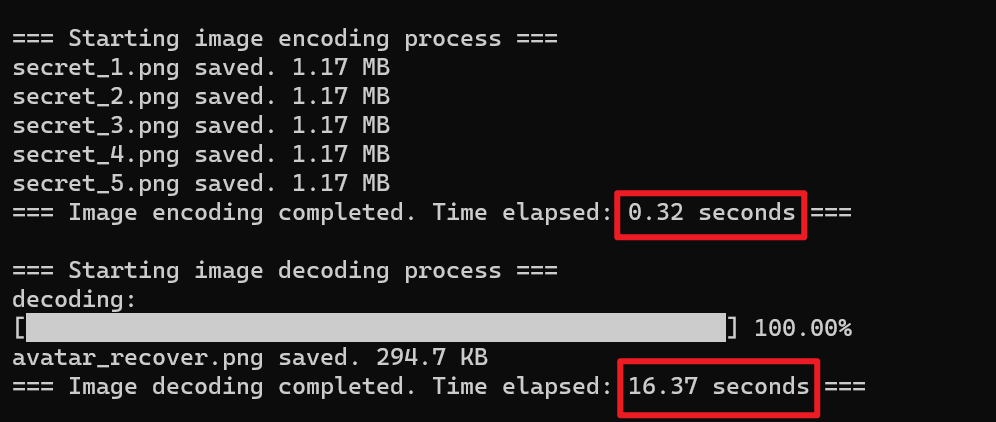
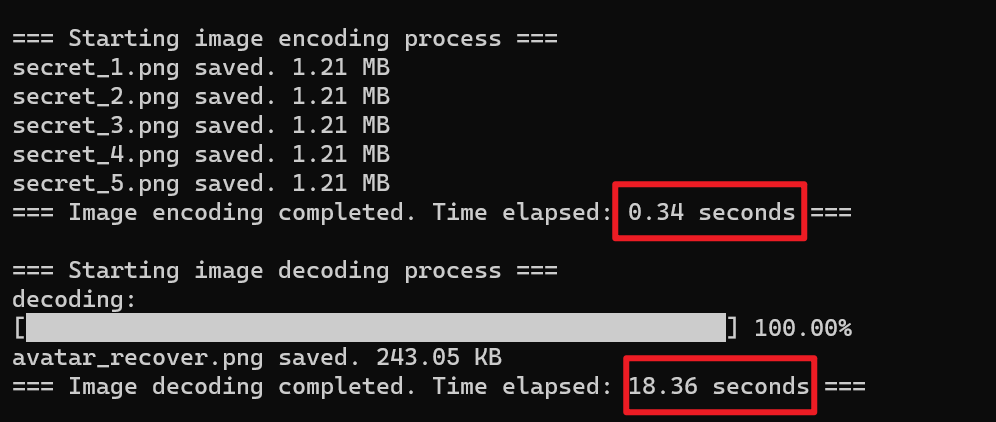
可以发现,添加了额外信息模块的算法运行时间变化不大,说明我们在元数据中添加信息的效率非常高,解码时余256点的恢复效率也很高
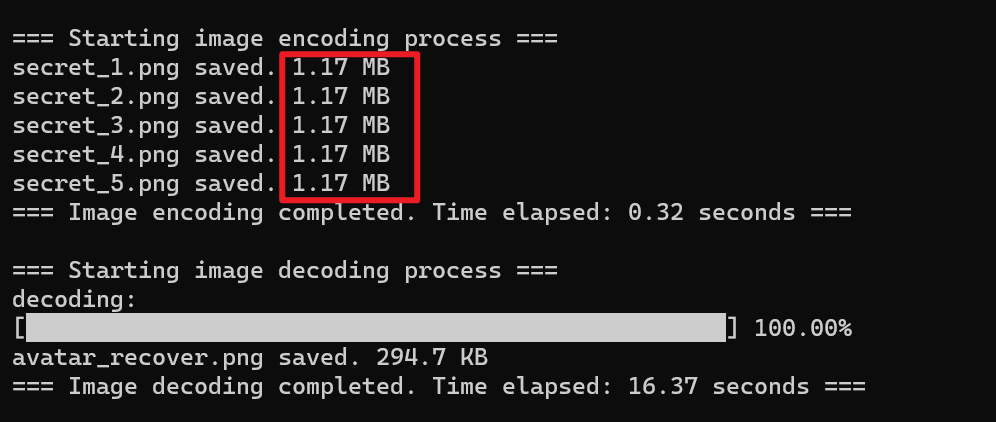
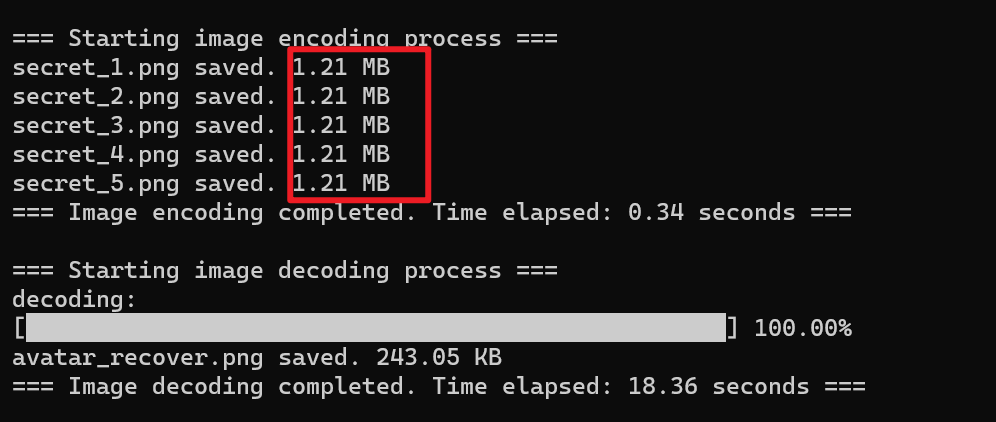
添加在元数据中的信息占影子图像大小的3%左右,说明我们添加的额外信息的信息密度非常高,保证了无损秘密共享的同时也不会消耗更多的空间资源