数字图像处理 人脸识别大作业

前言

本系列文章为学校课程《数字图像处理》布置的一些小project作业

除了给出每个问题的解答和代码，我也会附上相关知识点，以方便后续复习

前置概念

问题背景

给定一个人脸图像数据库和一个新的测试图像，我们如何才能直到测试图像包含了数据库中哪一个人的人脸

我们能想到的最简单的方法即计算测试图像与数据库中每一张人脸图像之间的SSD，找出差异最小的那张人脸

SSD(Sum of Squared Differences)，即平方差之和。这是一种常用于图像匹配和动作跟踪的技术。SSD通过计算两个图像或图像区域之间的像素强度差的平方和来衡量它们的相似性。数值越小，表示两个图像或区域越相似。SSD经常用于特征匹配、立体视觉和图像配准等领域，是一种简单而有效的方法来评估图像间的差异。

但这种方法显然存在很多问题，当我们比对两张人脸时，不能单单是比较图像的像素点是否一样

人脸识别领域存在着许多挑战：

1. 位置：人脸的图像可能并不在图像的正中心，此时我们比对两张图像的差异毫无意义
2. 大小与角度：人脸与摄影机直接的距离和角度会导致同一个人拍摄的人脸图像也有很大的变化量
3. 光照：光照条件的变化可以显著改变人脸的外观以及灰度值
4. 表情：不同的表情可以改变面部特征的外观
5. 年龄：随着时间的推移，人的面部特征会发生变化
6. 面部配饰：眼睛、胡子、围巾、耳环和发型的变化

那么我们显然需要比较不同图像中人脸的特征来判断身份

分析人脸特征有以下两种方法：

1. 检测可见的特征，例如眼睛、鼻子、嘴、脸颊、下巴、眉毛等。但是这种方法并不健壮
2. 统计整体方法：使用统计方法提取特征。这些特征不一定有物理上的解释

而传统数字图像处理领域的人脸识别方法即基于统计整体方法

下面会介绍两种方法：PCA人脸识别算法和Eigenfaces人脸识别算法

PCA

PCA也叫做主成分分析算法

主要思想：将n维特征映射到k维上，这k维是全新的正交特征也被称为主成分，是在原有n维特征的基础上重新构造出来的k维特征。

主要流程如下

1. 计算均值：对所有样本数据计算均值。

   $$\bar{x} = \frac{1}{N} \sum_{i=1}^{N} x_i$$

2. 去均值化（中心化）：每个样本减去均值，以确保数据以0为中心。

   $$x_i = x_i - \bar{x}$$

3. 计算协方差矩阵：计算去均值化后数据的协方差矩阵。

   $$C = \frac{1}{N-1} \sum_{i=1}^{N} (x_i - \bar{x})(x_i - \bar{x})^\top$$

4. 求解特征值和特征向量：计算协方差矩阵的特征值和特征向量。

   $$CV = V\Lambda$$

5. 选择主要成分：根据特征值的大小选择最重要的特征向量。

   $$\hat{V}_k = V(:,1:k)$$

6. 投影数据：将原始数据投影到选定的主成分上。

   $$\alpha_{ik} = \hat{V}_k^\top x_i$$

Eigenfaces

Eigenfaces基于PCA算法，也就是是PCA在人脸识别领域的应用

EigenFace方法利用PCA得到人脸分布的主要成分，具体实现是对训练集中所有人脸图像的协方差矩阵进行本征值分解，得对对应的本征向量，这些本征向量（特征向量）就是“特征脸”。每个特征向量或者特征脸相当于捕捉或者描述人脸之间的一种变化或者特性。这就意味着每个人脸都可以表示为这些特征脸的线性组合。

HW PCA人脸识别

作业要求：

1. 算法PCA人脸识别或Eigenfaces人脸识别（见人脸识别课件）

2. 采用数据库为剑桥大学ORL人脸数据库，包含40个人的400张人脸图像（每人对应10张），图像为92x112灰度图像（256灰度级），数据库：由主讲教师提供。

3. 对于每个人的10张图像，随机选择5张用来训练，另外5张用于测试。对于每人的5张训练图像，可以将5张训练图像平均后作为一个特征图像再进行PCA特征抽取。

4. 选择合适的特征维数，建议为50-100；采用2范数（欧式距离）最小匹配。

5. 对每个人的另外5张训练图像分别测试，共测试5x40个图像，计算识别系统的正确率 =（识别正确的图像数）/200。

6. 可以使用Matlab或Python的工具库。

处理数据集

首先我们需要先读取数据集并将图像矩阵与对应标签绑定

初始化训练集和测试集的数组

datasetPath = 'att_faces/';

% 初始化训练集和测试集
trainSet = [];
testSet = [];

% 加载数据集
for i = 1:40
    directory = sprintf('%ss%d/', datasetPath, i);
    for j = 1:10
        filename = sprintf('%s%d.pgm', directory, j);
        image = double(imread(filename));
        if j <= 5
            trainSet(:, :, end + 1) = image;
        else
            testSet(:, :, end + 1) = image;
        end
    end
end

这里需要注意的是，我们还需要移除声明数组时自动创建的第一个空元素

trainSet(:, :, 1) = [];
testSet(:, :, 1) = []; 

提取特征（主成分分析）

使用PCA算法是人脸识别中最关键的一步

在提取特征前，我们需要将同一人脸的5张训练图像平均后作为1个特征图像

avgImages = zeros(size(trainSet, 1), size(trainSet, 2), 40);

for i = 1:40
    avgImages(:, :, i) = mean(trainSet(:, :, (i-1)*5 + 1:i*5), 3);
end

我们使用平均方法mean()来获取平均矩阵

接下来则是PCA算法的流程

1. 计算均值：$\bar{x} = \frac{1}{N} \sum_{i=1}^{N} x_i$

   meanImage = mean(avgImages, 3);

   由于所给的图像已经是灰度图像，所以这一步其实可有可无

2. 去均值化（中心化）：每个样本减去均值，以确保数据以0为中心。

   $$x_i = x_i - \bar{x}$$

   shiftedImages = avgImages - repmat(meanImage, [1, 1, size(avgImages, 3)]);

   repmat()方法用于将meanImage数组的大小扩增到与avgImages一致

3. 计算协方差矩阵：计算去均值化后数据的协方差矩阵。

   $$C = \frac{1}{N-1} \sum_{i=1}^{N} (x_i - \bar{x})(x_i - \bar{x})^\top$$

   covarianceMatrix = cov(flatImages');

   使用matlab自带的cov()方法来计算协方差矩阵

4. 求解特征值和特征向量：计算协方差矩阵的特征值和特征向量。

   $$CV = V\Lambda$$

   xxxxxxxxxx1 1[eigenVectors, eigenValues] = eig(covarianceMatrix);

   使用matlab自带的eig()方法来计算特征向量与特征值

5. 选择主要成分：根据特征值的大小选择特征向量。

   $$\hat{V}_k = V(:,1:k)$$

   我们先将得到的特征值排序，选出最靠前的特征值大的k个特征向量

   [~, sortedIndices] = sort(diag(eigenValues), 'descend');
   eigenVectors = eigenVectors(:, sortedIndices);
   eigenVectors = eigenVectors(:, 1:k); 

投影数据到特征空间

由于测试数据后续要与训练集进行模板匹配，所以需要一起投影到特征空间

这里我们定义一个投影的函数

function projectedImages = projectToPCASpace(images, meanImage, eigenVectors)
    [rows, cols, numImages] = size(images);
    shiftedImages = images - repmat(meanImage, [1, 1, numImages]);
    flatImages = reshape(shiftedImages, rows * cols, numImages);
    projectedImages = eigenVectors' * flatImages;
end

$$\alpha_{ik} = \hat{V}_k^\top x_i$$

根据公式，我们将转置的特征向量乘到图像数组上即可

接着使用该函数将训练集与测试集均投影到特征空间

projectedTrainImages = projectToPCASpace(trainSet, meanImage, eigenVectors);
fprintf('训练集投影特征空间完毕\n');
projectedTestImages = projectToPCASpace(testSet, meanImage, eigenVectors);
fprintf('测试集投影特征空间完毕\n');

模板匹配

计算测试图像与训练图像在特征空间上的欧式距离，将其用作识别的判据

differences = projectedTrainImages - repmat(testImage, [1, size(projectedTrainImages, 2)]);
euclideanDistances = sum(differences.^2);
[~, closestImage] = min(euclideanDistances);
if ceil(closestImage / 5) == person
	personCorrectCount = personCorrectCount + 1;

选出其中欧氏距离最小的图像作为匹配结果，并判断是否与测试图像标签相同来计算准确率

测试

为了直观的显示中间结果，我们添加一段展示特征脸的代码

% 显示前20个特征脸
figure;
for i = 1:20
    % 提取第i个特征向量并重塑形状
    featureFace = reshape(eigenVectors(:, i), [rows, cols]);
    featureFace = rescale(featureFace);
    subplot(4, 5, i);
    imshow(featureFace);
    title(sprintf('特征脸 %d', i));
end

运行后可以得到下图

可以发现特征脸算是较为抽象的特征表示

接下来我们选取不同的特征维数来进行测试人脸识别准确率

我们只需将后续的投影以及模板匹配过程放在循环中即可

% 设置不同的特征维数进行测试
featureDimensions = 20:39;

% 存储每个维数的准确率
accuracies = zeros(size(featureDimensions));

for index = 1:length(featureDimensions)
    k = featureDimensions(index);
    
    % 提取前k个特征向量
    selectedEigenVectors = eigenVectors(:, 1:k);
    
    % 投影到PCA特征空间并人脸识别
    ...

    accuracy = correctCount / size(projectedTestImages, 2);
    accuracies(index) = accuracy;
    fprintf('特征维数 %d, 准确率: %.2f%%\n', k, accuracy * 100);
end

下面截取部分数据绘制成表格

特征维数	人脸识别准确率
32	88.00%
33	88.50%
34	89.00%
35	89.50%
36	89.00%
37	88.50%
38	88.50%

我们也可以将结果绘制成更直观的柱状图

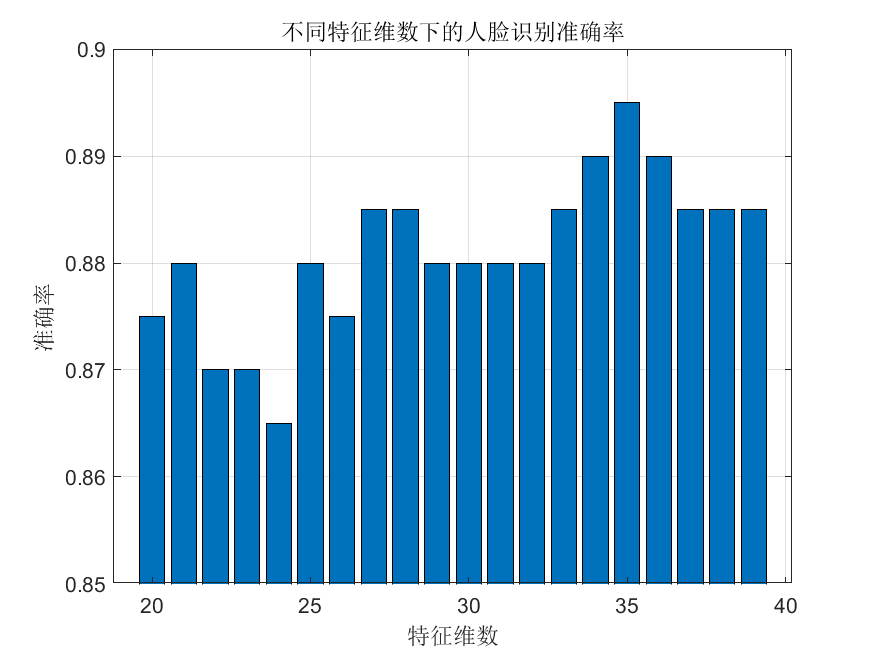
当特征维数为35时，准确率达到最高，这表明在这个维数下，选取的特征脸达到了最佳的泛化能力，有效地捕捉了人脸的关键特征，同时避免了过拟合。特征维数低于35时，可能由于特征信息不足，导致准确率下降，而高于35时，则可能由于引入不必要的噪声或冗余信息，导致准确率下降。

不平均图像的情况

当我们提取特征之前不对图片进行平均处理，此时可以获得更多的训练样本

在进行人脸识别之前，需要将同一id的人脸特征进行平均

for i = 1:40
    avgProjectedTrainImages(:, i) = mean(projectedTrainImages((i-1)*5+1:i*5, :), 1)';
end

我们再一次测试这种情况下特征数50-100的准确率

得到如下柱状图

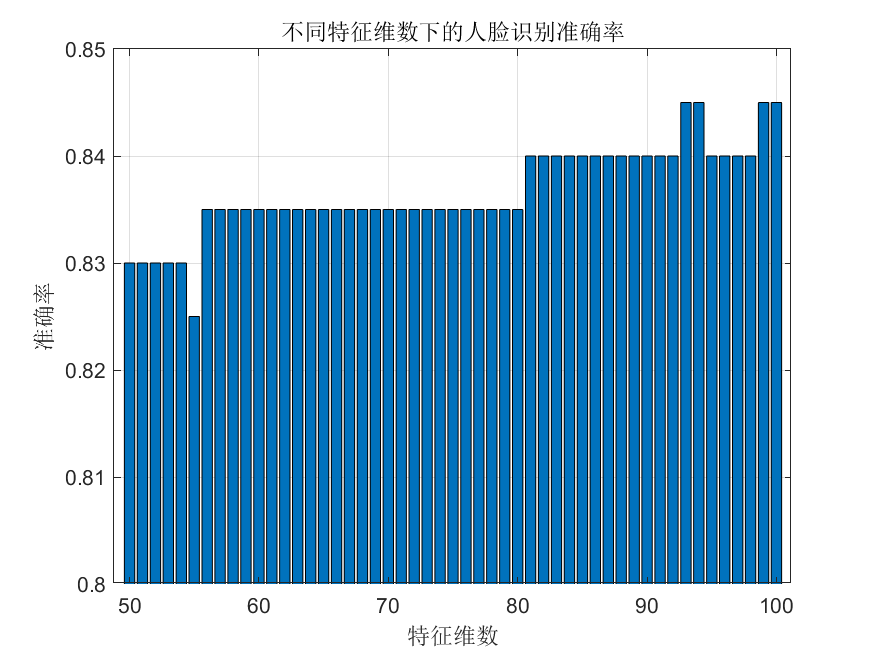
可以看到在93、94、99、100时达到最高准确率84.5%