同态加密

概述

在开始项目之前，我们需要回顾一下同态加密的知识

同态加密（Homomorphic encryption）是一种在加密数据上进行计算的技术，同时保证结果在解密后仍然有效。这种加密方法允许用户在不解密的情况下对加密数据进行操作，这在保护隐私的同时实现了数据的处理和分析。

同态加密的意义在于，真正从根本上解决将数据及其操作委托给第三方时的保密问题，例如对于各种云计算的应用。

同态加密的算法需要满足以下属性：

  1. 正确性：

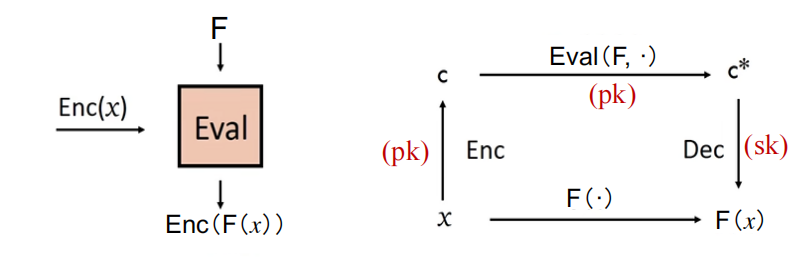
    • 对于未使用Eval函数的密文，如果$E$代表加密函数，$D$代表解密函数，$m$为明文，则正确性可以表示为：这意味着如果你对一个明文$m$进行加密，然后再解密，你应该得到原始的明文。
    • 对于使用Eval函数的密文，如果$F$代表在明文上的运算函数，正确性可以表示为：这表示如果你对多个加密后的数据应用Eval函数进行某种运算，然后解密，结果应该与在原始数据上直接应用该运算得到的结果相同。

  2. 隐私性：

    • 隐私性可以用不可区分性（indistinguishability）来表述。如果$m_1$和$m_2$是两个不同的明文，它们的加密结果（$E(m_1)$和$E(m_2)$）对于观察者来说应该是无法区分的。这通常表示为：

  3. 强同态：

    • 强同态属性要求加密数据和经过Eval函数求值后的密文在分布上应该是不可区分的。虽然这是理想状态，但在实际中很难实现，因此通常关注紧致性。

  4. 紧致性：

    • 紧致性关注的是密文尺寸的控制。如果$C$表示密文，$F$是计算函数，紧致性可以用以下方式表示：这意味着经过Eval函数处理后的密文大小是原始密文大小和计算函数复杂性的多项式函数，而不是与这些因素呈指数关系增长。

这些公式和属性共同定义了同态加密系统的基本特性，确保即使在加密状态下进行计算，也能保持数据的安全性和隐私性。

同态加密分为三类：部分同态加密（PHE）、近似同态加密（SHE）和全同态加密（FHE）

部分同态加密（PHE）

部分同态加密允许对加密数据执行一种类型的算术运算，通常是加法或乘法。在这种加密系统中，可以对加密数据进行无限次指定类型的运算

加法同态

在定义上，设$E$表示加密函数，$D$表示解密函数，$m_1$和$m_2$表示两个明文。如果系统是加法同态的，那么有：

$\begin{align}
D(E(m_1) \oplus E(m_2)) &= m_1 + m_2
\end{align}$

其中，⊕表示在加密数据上进行的某种操作，它相当于明文上的加法。

加法同态加密的代表算法是Paillier

Paillier加密算法是一种流行的非对称加密算法，由法国密码学家Pascal Paillier于1999年提出。

其安全性依赖于合数剩余判定假设

合数剩余判定假设（CRA）是基于对特定合数的剩余类的难以区分性。具体来说，假设有两个大质数$p$和$q$，则对于模$n^2$（其中$n = pq$）的乘法群，很难区分一个随机选择的群元素是否是模$n^2$的$n$次幂。

在数学术语中，如果$x$是一个随机选择的模$n^2$的群元素，则区分$x$是不是一个$n$次剩余（即存在某个$y$使得$y^n \equiv x \mod n^2$）是困难的。

具体加解密流程如下：

与传统的加法同态操作有所不同，Paillier加密系统中，明文的加法操作对应于密文的乘法操作

乘法同态

同样地，设$E$表示加密函数，$D$表示解密函数，$m_1$和$m_2$表示两个明文。如果系统是加法同态的，那么有：

$\begin{align}
D(E(m_1) \otimes E(m_2)) &= m_1 \times m_2
\end{align}$

比较具有代表性的乘法同态加密算法是RSA和ElGamal

近似同态加密（SWHE）

近似同态加密是一种介于PHE和FHE之间的加密形式。它支持对加密数据进行有限次的加法和乘法操作。然而，随着计算次数的增加，密文中的噪声也会增加，限制了可以执行的操作次数。

代表性的算法有下面几种

下面是BGN的具体原理和算法流程

全同态加密(FHE)

全同态加密是同态加密的最强形式，允许对加密数据执行无限次的加法和乘法运算。它使得在保持数据加密的情况下进行复杂计算成为可能。

全同态加密（FHE）的一个关键特性是其自举（bootstrapping）能力，这个概念是由Craig Gentry在他的博士论文中首次提出的。自举是一种技术，它使得全同态加密系统能够处理任意数量的计算操作，而不受到噪声的限制

自举是指在同态加密环境中，加密方案可以使用自己来刷新自己的密文。在同态加密操作中，计算会在密文中引入噪声。如果噪声积累到一定程度，将导致密文无法正确解密。自举技术允许对密文进行处理，以减少这种噪声，从而可以继续进行更多的计算操作。

这种操作可以递归地进行。也就是说，一个全同态加密方案可以对其自身的加密计算进行同态加密，并通过自举来去除在此过程中引入的噪声。

实现自举需要加密方案能够对其解密过程进行同态评估。这通常涉及到：

  • 将解密算法表示为一个低复杂度的算术电路。

  • 使用同态加密方案来加密该电路的输入（即密文和解密密钥的加密版本）。

  • 运行同态加密的解密电路，这样做会生成一个新的加密版本的密文，其中包含较少的噪声。

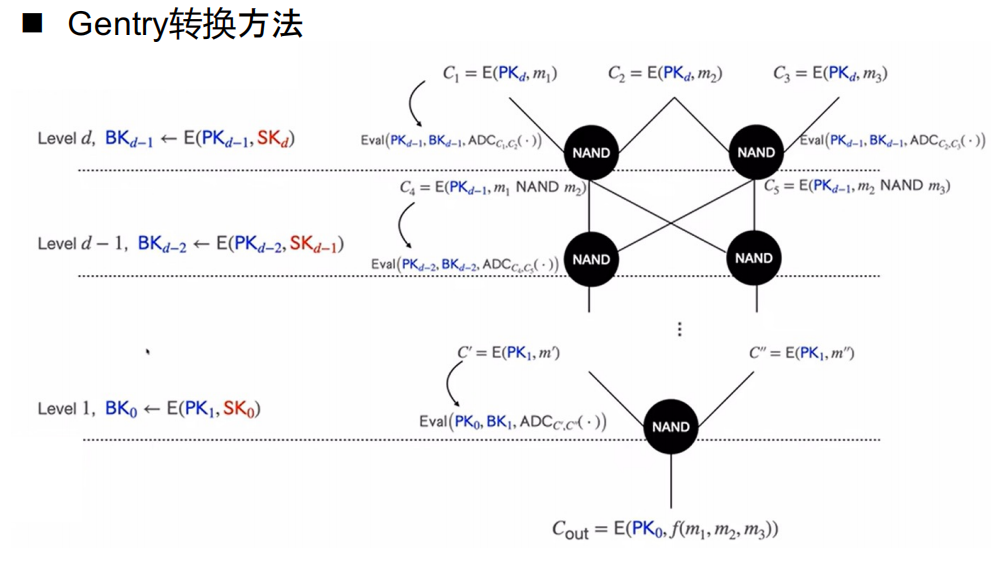
第一代FHE

Gentry的方案被视为第一代FHE。它首次提出了自举（bootstrapping）的概念，即通过自解密来减少密文中的噪声。Gentry的构造基于理想格，并为未来的FHE构造提供了原型。

算法原理如下

其建立在AGCD困难问题上

由于要满足正确性成立条件，该算法只支持次数较低的多项式密文运算，原因如下：

假设$ B=O(2^\lambda) $为fresh密文的噪音边界，则经过$d$层的乘法电路之后，噪音边界变为$ B^{2^d} $，则有：

第一代FHE的缺点在于整数的尺度非常大，导致效率非常低

第二代FHE

第二代FHE的代表性算法为BGV

建立在困难问题LWE上

第二代FHE的特殊之处在于它在减小误差项上做出了探索
主要方法有两种，密钥交换和模块交换

密钥交换是一种在FHE中常用的技术，它允许将一个密文从一个密钥空间转换到另一个密钥空间，而不会解密密文本身。

首先生成一个包含旧密钥加密的新密钥的数据结构，这通常是通过旧密钥对新密钥的每个位进行加密得到的。然后通过这个数据结构将加密数据从旧密钥转换为新密钥的形式，这一步骤不涉及明文数据的解密过程。通过精心设计的密钥交换过程，可以限制或减少转换过程中引入的误差。

模块交换将密文中的每个系数从一个大模数环切换到一个小模数环，这通常也会减少误差项的大小。针对同一个明文消息，将在模q下的密文c转换成在模p下的密文c’ ，可将同态加密累积误差总量减少约p/q倍

第三代FHE

第三代FHE的代表算法是GSW

其核心思想是利用矩阵的近似特征向量

基础方案如下

但是通过线性代数方法，能够很容易找到C的特征向量与点对应的特征值，从而轻松破解该方案的加密体系

我们可以加入随机噪声

但是仍然有缺点

改进方案是利用二进制分解

第四代FHE

第四代FHE的代表性算法是CKKS

它的特点是支持浮点数运算

开源库算法效率比较

项目设计

本实验选择使用TenSEAL作为开源同态加密库，其代码托管于GitHub，链接如下：

TenSEAL：https://github.com/OpenMined/TenSEAL

该同态加密的开源库中实现了BFV和CKKS这两种全同态加密算法

实验流程如下：

  1. 环境安装：安装开源库TenSEAL及其依赖环境
  2. 准备测试数据：搜集一组图片当作测试数据，并将其预处理为64*64的分辨率
  3. 加密数据：将测试图片使用选定的算法加密，记录花费的时间
  4. 存入数据库：将加密数据与对应标签存入数据库
  5. 查询匹配：加密查询图片，将其与数据库中的加密图像依次匹配，选取其中最相似的图片，并将其解密并展示，记录匹配的时间以及解密的时间，
  6. 分析对比算法效率：分析各步骤的时间，以对比不同算法的效率和优缺点。

其中第2、3、4、5步需要对不同算法重复进行

这里我们还需要明确加解密的流程

因为我们想要模拟一个查询图片服务的现实场景

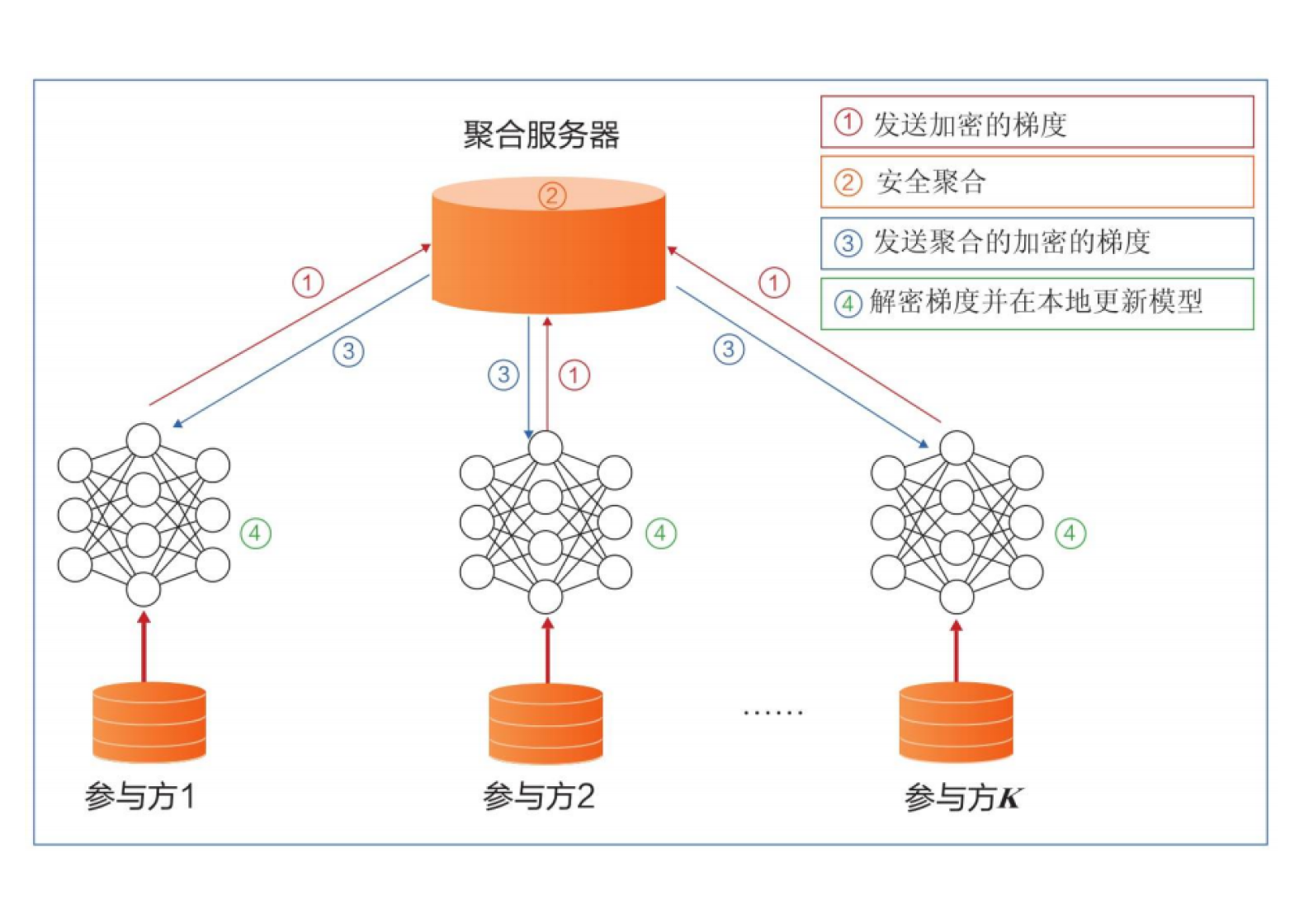
加密图片会储存在服务端的数据库，而需要匹配的图片则由用户端提供

在这种角色关系中，服务端相当于权威方，所以一开始的公私钥生成在服务端进行

服务端使用公钥加密存储的图片，并将公钥分发给客户端，将私钥保留

客户端使用公钥加密测试图片后发送給服务端，服务端将其与数据库中的加密图片匹配，找到最相似的一张后使用私钥解密得到原图并返回给客户端

整个过程可以用以下流程图来表示

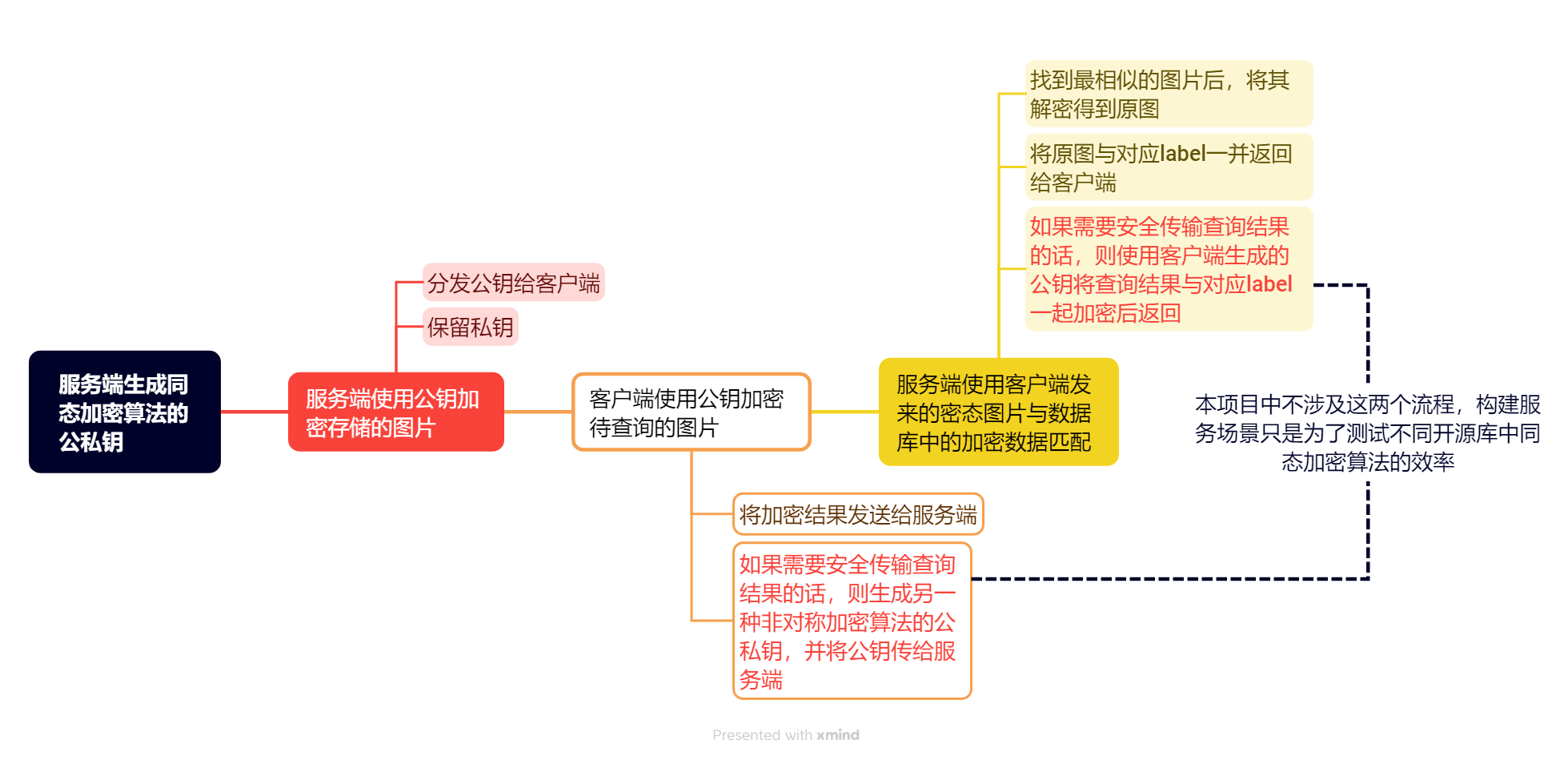
当然这只是模拟现实世界的一种场景，在其他方案中公私钥的保存者和数据传输状态都不是固定的，本方案中弱化了对用户提供的数据的保护（可以通过额外的加密算法来提供安全性），而是将保护重心放在了数据库存储的图片上。

在我们的方案中，同态加密具体体现在图片的密态匹配过程，若原图的相似度最高，则密态下计算出的相似度也是最高的

环境安装

创建一个新的python环境，并使用pip安装TenSEAL

1
2
3
conda create -n TenSEAL python=3.8
conda activate TenSEAL
pip install tenseal

准备测试数据

为了模拟现实场景中同态加密存储隐私信息的应用，我们使用CelebA(CelebFaces Attribute)数据集中的2500张人脸图片作为测试数据

下面是数据集的下载地址

https://pan.baidu.com/s/1eSNpdRG#list/path=/

我们选择Img/img_align_celeba.zip，即经过裁剪的JPG格式数据集

选取前2500张图片存入数据库

此时图片分辨率为178*218

我们可以写一个python脚本将图片裁剪压缩为64*64

在环境中安装图像处理库Pillow

1
pip install Pillow

我们使用crop()方法来裁剪图片，然后使用resize()进行缩放

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
from PIL import Image
import os

def resize_images(folder_path, output_folder, output_size=(64, 64)):
    if not os.path.exists(output_folder):
        os.makedirs(output_folder)

    for filename in os.listdir(folder_path):
        if filename.lower().endswith(('.png', '.jpg', '.jpeg')):  # 或者根据实际情况调整文件格式
            image_path = os.path.join(folder_path, filename)
            output_path = os.path.join(output_folder, filename)

            with Image.open(image_path) as img:
                min_side = min(img.width, img.height)
                # 计算裁剪区域
                left = (img.width - min_side) / 2
                top = (img.height - min_side) / 2
                right = left + min_side
                bottom = top + min_side

                # 裁剪和缩放
                img_cropped = img.crop((left, top, right, bottom))
                img_resized = img_cropped.resize((output_size))

                # 保存处理后的图片
                img_resized.save(output_path)

resize_images('data/storage_imgs', 'data/storage_imgs')

同时，我们截取Anno/identity_CelebA.txt和Anno/list_attr_celeba.txt的前1000项数据作为label

加密数据

一开始处理图像时，我们将其转换为numpy数组，这需要我们安装numpy库

1
pip install numpy

对于加密算法，我们需要进行判断，因为不同的算法初始化上下文时的参数不同

1
2
3
4
5
6
7
8
9
if args.context:
    context = load_context(args.context)

else:
    if args.algorithm == 'BFV':
        context = ts.context(ts.SCHEME_TYPE.BFV, args.poly_modulus_degree, args.plain_modulus)
    elif args.algorithm == 'CKKS':
        context = ts.context(ts.SCHEME_TYPE.CKKS, args.poly_modulus_degree)
        context.global_scale = args.global_scale

当然如果已经提供了带公钥的的上下文，我们直接赋值即可

接下来是生成并保存公私钥

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def save_context(context, file_path):
    with open(file_path, "wb") as f:
        f.write(context.serialize(save_secret_key=True))
...
# 生成公私钥
context.generate_galois_keys()

# 序列化并保存包含私钥的上下文
save_context(context, os.path.join(keys_folder, "private_context"))

# 移除私钥
context.make_context_public()

# 序列化并保存公钥上下文
save_context(context, os.path.join(keys_folder, "public_context"))

在保存为上下文的文件时，我们可以使用serialize方法将上下文序列化，同时我们要设置save_secret_key为true，这样能保证私钥上下文在序列化时依然保留私钥

首先我们需要读取待加密的图片，并将其碾平为一维数组

1
2
3
4
5
# 加载图片并转换为 numpy 数组
with Image.open(image_path) as img:
    img_data = np.array(img)
    
img_data_flattened = img_data.flatten()

BFV和CKKS的加密函数分别为bfv_vector和ckks_vector，我们将上下文context和待加密的图像数组即可

1
2
3
4
5
6
if algorithm == 'BFV':
    encrypted_data = ts.bfv_vector(context, img_data_flattened.tolist())  # 加密整个向量
elif algorithm == 'CKKS':
    encrypted_data = ts.ckks_vector(context, img_data_flattened.tolist())
else:
    raise ValueError("Unsupported algorithm. Please choose 'BFV' or 'CKKS'.")

最后我们将加密数据序列化后保存

1
2
3
4
5
6
7
encrypted_data_serialize = encrypted_data.serialize()

encrypted_filename = os.path.splitext(os.path.basename(image_path))[0] + "_encrypted"
encrypted_file_path = os.path.join(output_folder, encrypted_filename)

with open(encrypted_file_path, "wb") as f:
    f.write(encrypted_data_serialize)

当然，在加密时，我们使用python自带的time库来统计加密时间

1
2
3
4
start_time = time.time()  # 开始计时
...
end_time = time.time()
encryption_time = end_time - start_time

在代码最后统计并输出总加密时间以及单张图像的加密时间

1
2
3
4
5
6
7
8
total_time, count = encrypt_images_in_folder(args.input_folder, args.algorithm, context, args.output_folder)
if count > 0:
    average_time = total_time / count
    print(f"Total encryption time: {total_time:.3f} seconds")
    print(f"Average encryption time per image: {average_time:.3f} seconds")
    print(f"Number of images encrypted: {count}")
else:
    print("No images were encrypted.")

存入数据库

在数据库上，我们选用SQLite来模拟数据的存储场景

选择SQLite而非MySQL的原因主要是本项目的规模较小，且SQLite搭建时更加方便，最重要的是python内置sqlite3库

在现实场景中，一个用户之所以使用查询图片服务，当然是希望获取这张图片的一些信息

所以在数据库中的每一项，我们除了存入加密的图片向量，还需要存入该图片的一些label

正好CelebA提供人像图片的特征标签以及身份标签，即Anno/list_attr_celeba.txt和Anno/identity_CelebA.txt两个文件

首先创建数据库

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def create_database(db_name):

    print(f"=== Creating database:{db_name} ===", )
    if os.path.exists(db_name):
        # 如果存在，则删除该文件
        os.remove(db_name)
        print("Existing database removed.")

    conn = sqlite3.connect(db_name)
    cursor = conn.cursor()
    cursor.execute('''
        CREATE TABLE IF NOT EXISTS images (
            filename TEXT PRIMARY KEY,
            identity TEXT,
            attributes TEXT,
            encrypted_data BLOB
        )
    ''')
    conn.commit()
    conn.close()
    print("=== Database created successfully. ===\n")

我们在处理图像前处理两个文件中的标签，存为数据结构

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def parse_identity_file(file_path):
    identity = {}
    with open(file_path, "r") as file:
        for line in file:
            parts = line.strip().split()
            identity[parts[0]] = parts[1]
    return identity

def parse_attr_file(file_path):
    attributes = {}
    with open(file_path, "r") as file:
        # 读取并忽略第一行
        next(file)
        attr_names = file.readline().strip().split()
        for line in file:
            parts = line.strip().split()
            attributes[parts[0]] = dict(zip(attr_names, parts[1:]))
    return attributes
...
identity_data = parse_identity_file("Anno/identity_CelebA.txt")
attr_data = parse_attr_file("Anno/list_attr_celeba.txt")
# 处理图像
process_images(args.input_folder, args.database, identity_data, attr_data)

在加密完图片后，查找该图片的标签，并将加密数据与对应标签一并存入数据库

1
2
3
4
5
6
7
identity = identity_data.get(image_filename)
attributes = attr_data.get(image_filename)
if identity is not None and attributes is not None:
    image_path = os.path.join(input_folder, filename)
    with open(image_path, "rb") as f:
    	encrypted_data = f.read()
    insert_into_database(db_name, image_filename, identity, attributes, encrypted_data)

查询匹配

由于余弦相似度的计算设计除法，在获得最终结果前必须解密，所以我们选择使用欧几里得距离来表示图像间的相似性

图像矩阵A和B之间的欧式距离计算公式如下

$d(\mathbf{A}, \mathbf{B}) = \sqrt{\sum_{i=1}^{n} (A_i - B_i)^2}$

由此我们可以写出匹配的代码

1
2
3
4
5
6
7
8
9
10
11
def compute_euclidean_distance(enc1, enc2, context):
    sk = context.secret_key()
    
    # 计算两个向量的差异
    diff_enc = enc1 - enc2
    diff = diff_enc.decrypt(sk)
    # 计算差异的平方
    diff_squared = [x**2 for x in diff]
    diff_squared_sum = sum(diff_squared)

    return diff_squared_sum

如果找到最佳匹配图像后，我们需要显示这个图像的一些相关信息

包括相似度

我们需要额外写一个函数，将欧氏距离转化为相似度百分数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def distance_to_similarity(distance, max_distance):
    if distance >= max_distance:
        return 0
    else:
        return (1 - distance / max_distance) * 100
...

if best_match:
    decrypted_image = decrypt_image(best_match[1], algorithm, context)
    similarity = distance_to_similarity(min_distance,max_distance)
    output_filename = os.path.splitext(query_filename)[0] + "_matched_with_" + os.path.splitext(best_match[0])[0] + ".jpg"
    output_file_path = os.path.join(output_folder, output_filename)
    Image.fromarray(decrypted_image).save(output_file_path)
    print(f"Query image '{query_filename}' best matches with database image '{best_match[0]}'")
    print(f"Similarity is '{similarity:.2f}%'")
    identity_tag, feature_tags = get_image_tags(db_name, best_match[0])
    print(f"Identity Tag: {identity_tag}")
    print(f"Feature Tags: {', '.join(feature_tags)}\n")
    print("=== Matching and decryption completed. ===\n")

创新点

模拟现实场景

在本项目中，我们特别注重模拟真实世界中的数据处理和隐私保护场景。通过构建一个包含同态加密和图像匹配的完整流程，我们模拟了一个现实场景中的图像查询和匹配服务。这不仅展示了同态加密技术的实用性，也为数据隐私保护提供了切实可行的解决方案。

在这个模拟的场景中，我们明确区分了服务端和客户端的角色。服务端负责图像数据的加密存储和匹配处理，而客户端则负责提供查询图像。通过这种角色分配，我们能够展示在数据隐私保护的背景下，如何在服务端和客户端之间安全地交换和处理信息。

通过选项--context的设置，加密程序以及匹配程序能够使用之前程序产生的密钥文件，这一点对于模拟真正场景下的密钥分配至关重要

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
def load_context(file_path):
    print("Loading context from: ", file_path)
    with open(file_path, "rb") as f:
        return ts.Context.load(f.read())
...
if args.context:
        context = load_context(args.context)
else:
        if args.algorithm == 'BFV':
            context = ts.context(ts.SCHEME_TYPE.BFV, args.poly_modulus_degree, args.plain_modulus, coeff_mod_bit_sizes=[60, 40, 40, 40, 40, 60])
        elif args.algorithm == 'CKKS':
            context = ts.context(ts.SCHEME_TYPE.CKKS, args.poly_modulus_degree, coeff_mod_bit_sizes=[60, 40, 40, 40, 40, 60])

            context.global_scale = args.global_scale
        # 生成公私钥
        context.generate_galois_keys()
        # 序列化并保存包含私钥的上下文
        save_context(context, os.path.join(keys_folder, "private_context"))
        # 移除私钥
        context.make_context_public()
        # 序列化并保存公钥上下文
        save_context(context, os.path.join(keys_folder, "public_context"))

同时，我们的系统设计允许在完全保护图像数据隐私的前提下进行高效的图像匹配。通过使用同态加密技术，所有图像数据（包括数据库中的图像和查询图像）都在加密状态下进行处理。这种方法确保了即使在数据传输或存储过程中发生安全漏洞，图像内容也不会泄露。

优化的加密数据存储结构

全同态加密加密后的数据体积显著增加。为了解决这个问题，需要选择合适的方式存储加密数据。相比于直接将加密后的数据和annotations存在文件系统中，存在数据库中时的存储效率更高，而且在匹配查询时能更快捷的查找到相应数据的标签。

本算法使用DBUploader.py脚本将加密后的图像数据和对应的标签信息存储到SQLite数据库中。数据库设计上，我们创建了一个表来存储加密的图像数据和标签。这个表包含以下几个字段：图像文件名、加密图像数据、图像的标签信息。

1
2
3
4
5
6
7
8
9
10
for i, filename in enumerate(files):
        file_number = re.sub('[^0-9]', '', filename)
        image_filename = file_number + '.jpg'
        identity = identity_data.get(image_filename)
        attributes = attr_data.get(image_filename)
        if identity is not None and attributes is not None:
            image_path = os.path.join(input_folder, filename)
            with open(image_path, "rb") as f:
                encrypted_data = f.read()
            insert_into_database(db_name, image_filename, identity, attributes, encrypted_data)

这里，我推荐使用DB Broswer(SQLite)来观察和验证生成的数据库文件

通过选项来调整加密算法及参数

在本项目中，我们实现了一种灵活的加密算法选择机制。通过命令行选项或程序界面，用户可以根据需要选择不同的同态加密算法（如BFV或CKKS）。这种动态选择机制使得项目能够适应不同的应用场景和安全需求。

除了选择不同的加密算法外，用户还可以调整各种加密参数，如多项式模数度（poly_modulus_degree）、明文模数（plain_modulus）和全局比例因子（global_scale）。这些参数对加密的性能和安全性有着直接影响。在实验测试的过程中，我们不需要修改源文件，而是简单地输入不同参数选项即可调整算法参数。

在代码层面，这一功能是通过解析用户输入的参数实现的。例如，在tenseal_encrypt.py脚本中，得益于Python的argparse库，我们可以很方便地接收和处理用户输入的加密算法和参数选项。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
import argparse

parser = argparse.ArgumentParser()
parser.add_argument("-a", "--algorithm", choices=["BFV", "CKKS"], help="Encryption algorithm to use")
parser.add_argument("-p", "--poly_modulus_degree", type=int, help="Polynomial modulus degree")
parser.add_argument("-m", "--plain_modulus", type=int, help="Plaintext modulus (for BFV)")
parser.add_argument("-s", "--global_scale", type=int, help="Global scale (for CKKS)")
args = parser.parse_args()

# 根据用户选择设置加密算法和参数
if args.algorithm == "BFV":
    # 设置BFV算法参数
elif args.algorithm == "CKKS":
    # 设置CKKS算法参数

当然，还有一些选项供用户选择原图像的目录、加密数据的存储目录等

显示直观且详细

我们通过精确测量加密、匹配以及解密过程中每一步骤所消耗的时间，为用户提供了一个明确的性能指标。例如，记录加密单张图片所需的时间，可以帮助用户理解不同参数设置对加密速度的影响。为了提高用户体验，在处理大量数据时，我们实现了一个进度条来直观地展示当前操作的进度。在图像匹配过程中，除了展示匹配结果，我们还提供了匹配图像的详细标签信息。这一点在测试算法效率时尤为重要，因为它不仅显示了哪些图像被匹配到，还提供了关于匹配质量的额外信息。

具体实现如下：

  1. 时间展示：

    在每个步骤开始前记录当前时间，步骤结束后再次记录时间，通过两者的差值计算步骤耗时

    1
    2
    3
    4
    5
    6
    7
    8
    import time

    start_time = time.time()
    # 加密或其他处理过程
    end_time = time.time()

    elapsed_time = end_time - start_time
    print(f"该步骤耗时: {elapsed_time}秒")

  2. 进度条显示：

    对于处理大量数据的情况，通过进度条来展示完成进度很有必要，我们没有使用现成的tqdm库，而是手搓了一段进度条代码，主要是为了方便控制进度条增长的条件（当数据很多时，可以设置每隔1%进度条增长一次）

    1
    2
    3
    4
    5
    6
    7
    # 更新进度条
    percent_done = (i + 1) / total_files
    bar_length = 50
    block = int(bar_length * percent_done )
    text = "\r[{}{}] {:.2f}%".format("█" * block, " " * (bar_length - block), percent_done*100)
    sys.stdout.write(text)
    sys.stdout.flush()

  3. 标签信息：

    在图像匹配过程中，除了显示匹配结果外，还可以显示匹配图像的详细标签信息，这有助于用户更全面地评估匹配算法的效果。

    1
    2
    3
    4
    5
    6
    7
    8
    # 从数据库中提取标签信息
    def get_image_tags(image_id):
        # 数据库查询逻辑
        return identity_tag, feature_tags

    identity_tag, feature_tags = get_image_tags(db_name, best_match[0])
    print(f"Identity Tag: {identity_tag}")
    print(f"Feature Tags: {', '.join(feature_tags)}\n")

实验及分析

实验环境

下面是进行实验时，本机的配置

  • CPU: AMD Ryzen 7 5800H
  • GPU: NVIDIA RTX 3070 Laptop 8G
  • Memory: 16GB
  • Operating System: Windows10
  • Python Version: 3.8.18

我们依次对已有图像数据进行加密、存入数据库、查询匹配的操作，并比对不同算法的效率

首先测试BFV的时间

BFV

BFV的加密参数如下所示，我们需要保证加密容量能够允许加密64*64*3大小的图像向量

1
2
3
poly_modulus_degree = 32768
plain_modulus = 65537
coeff_mod_bit_sizes=[60, 40, 40, 40, 40, 60]

首先我们模拟服务端对数据的初始化操作，即加密图像数据并存入数据库

执行如下指令，对图像进行BFV全同态加密

1
python tenseal_encrypt.py -a BFV -i data/storage_imgs -o data/enc_storage_imgs

这里使用的是默认参数，当然也可以直接指定参数

1
python tenseal_encrypt.py -a BFV -i data/storage_imgs -o data/enc_storage_imgs -p 32768 -m 65537

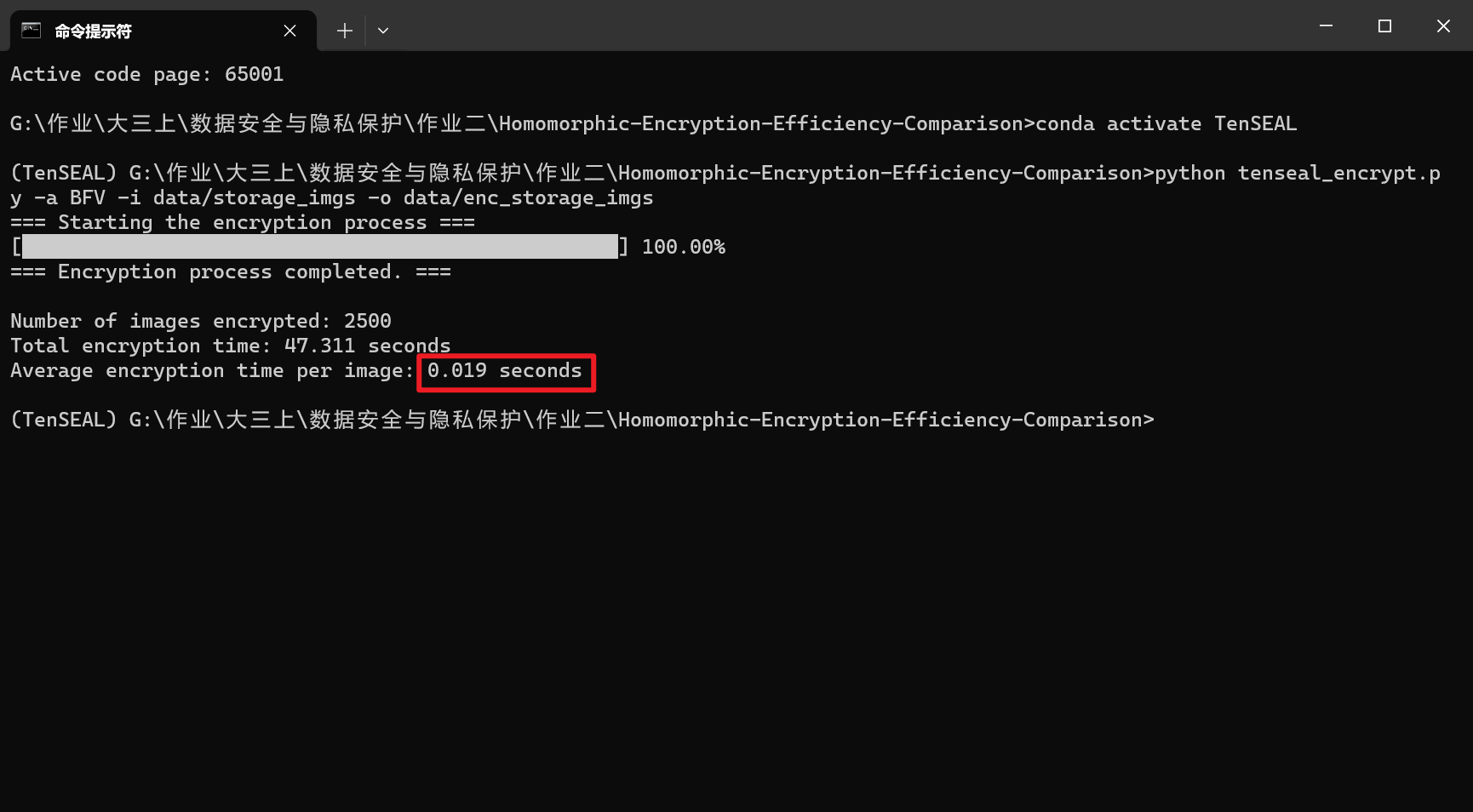
统计得到单张图像的加密时间为0.019秒

在keys目录下我们可以查看到上下文初始化得到的公钥和私钥

在我们选择的输出目录data/enc_storage_imgs下可以查看加密后的数据

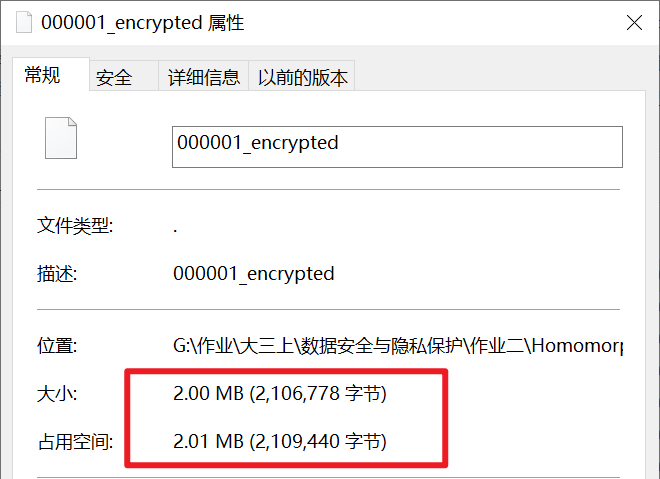
单张图片的加密数据大小为2MB，约为原图像大小的1000倍

运行DBUploader.py程序，将加密数据存入SQLite数据库，这里在项目根目录下生成数据库文件

1
python .\DBuploader.py -i .\data\enc_storage_imgs\

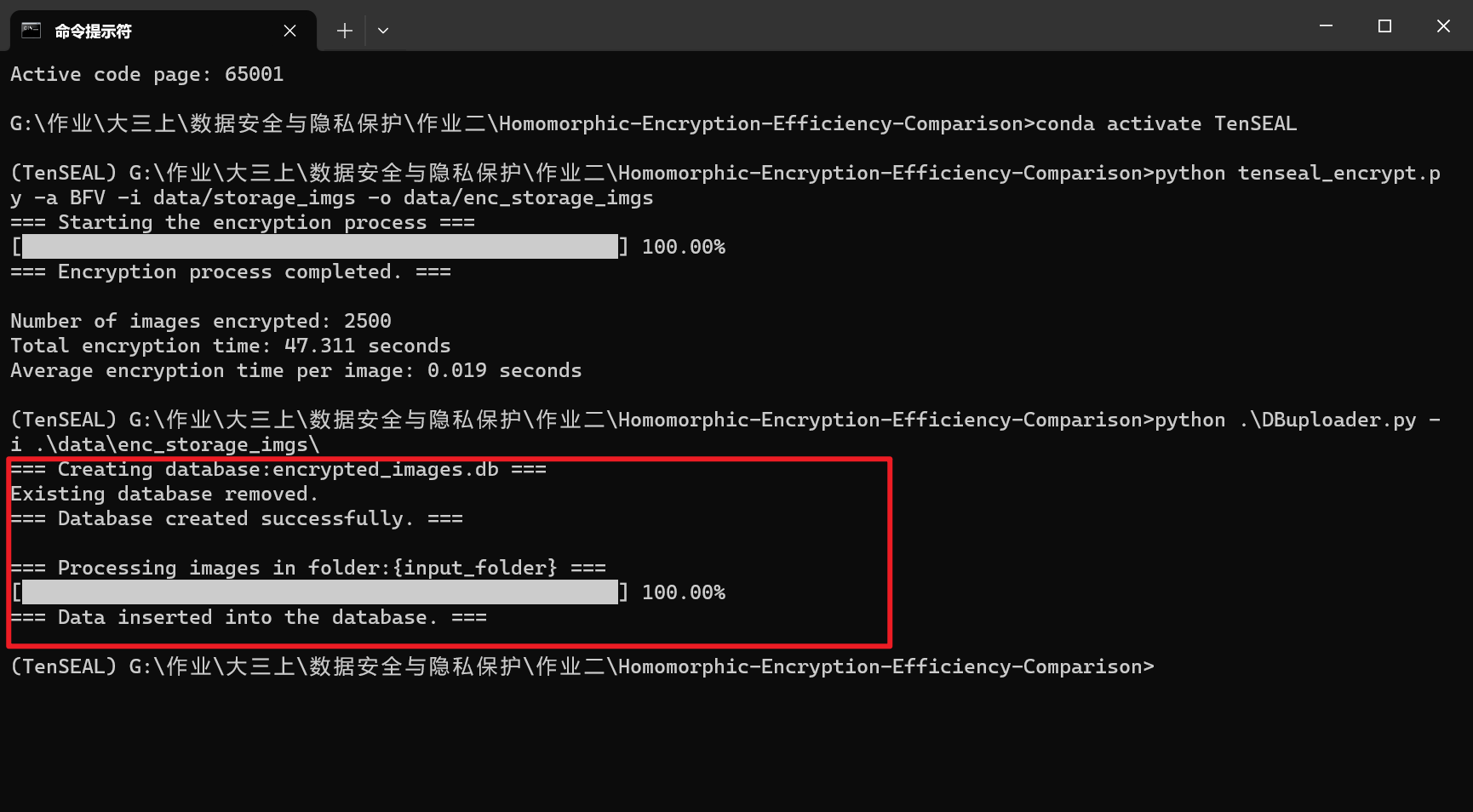
可以观察到成功生成了数据库文件encrypted_images.db

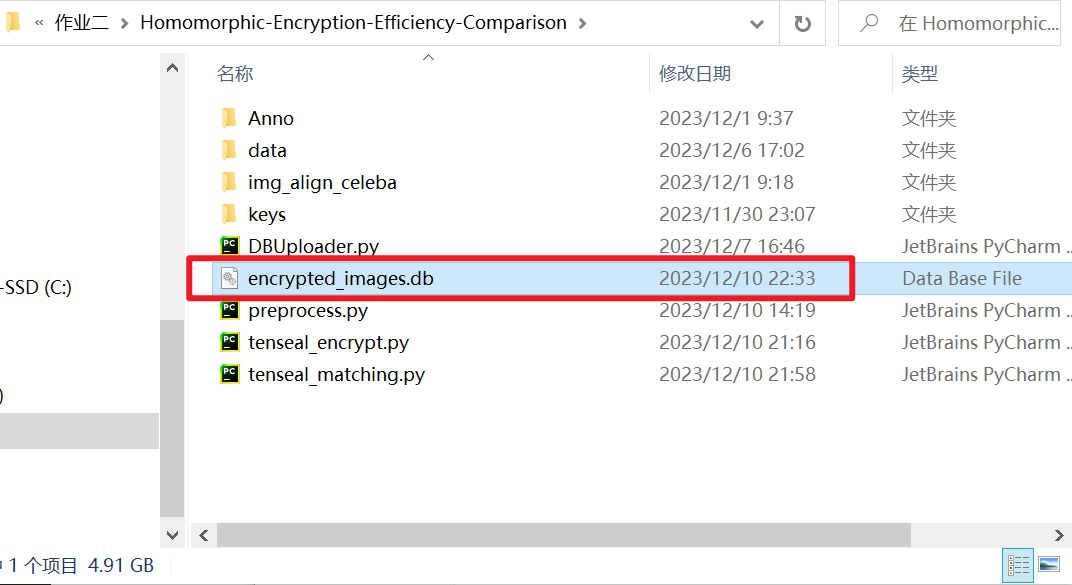
接下来我们模拟用户端的操作

将data/matching_imgs文件夹下的待匹配图像加密

1
python tenseal_encrypt.py -a BFV -i data/matching_imgs -o data/enc_matching_imgs -c .\keys\public_context

这里使用的是前面指令在keys目录下生成的公钥

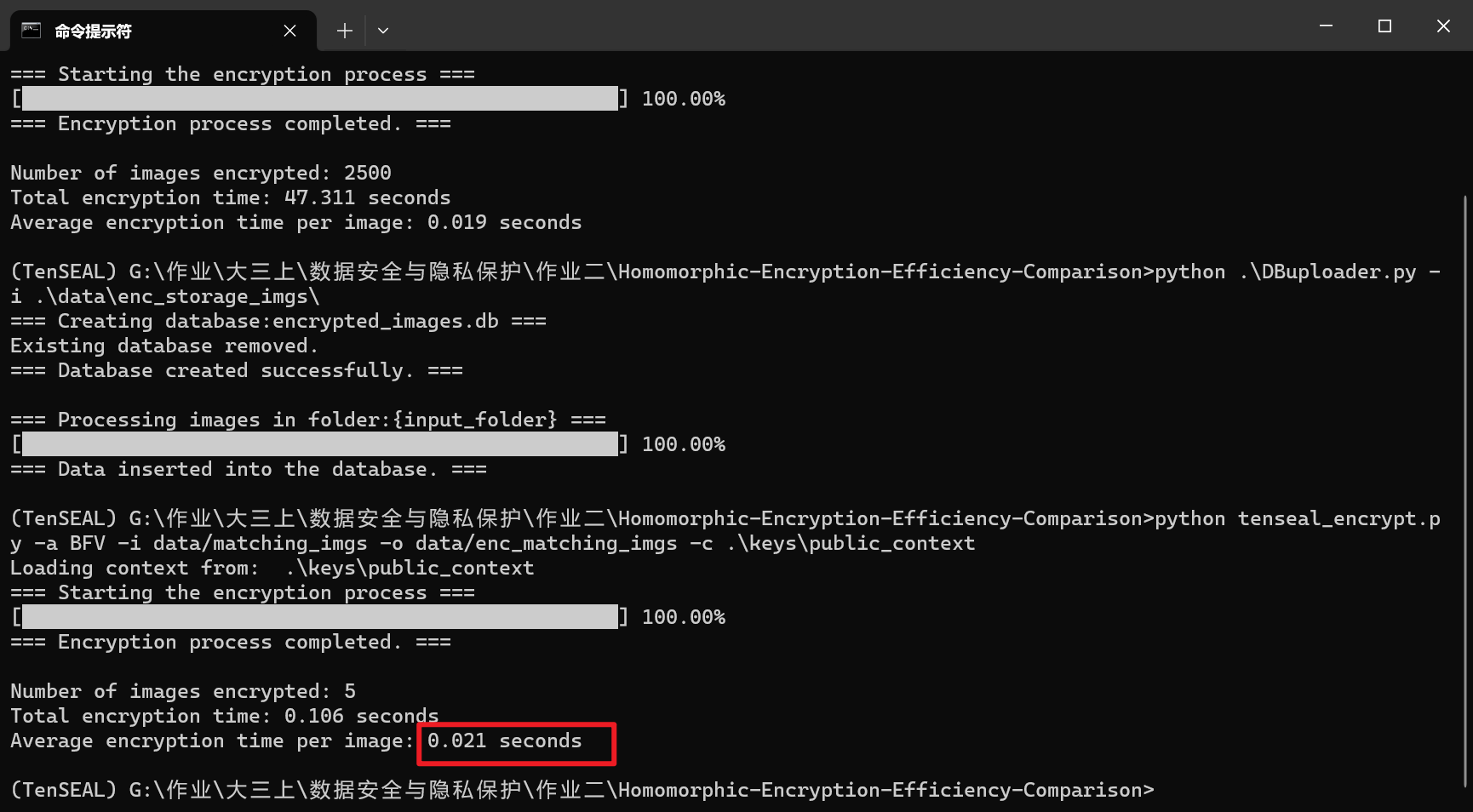
加密待匹配图像时单张图像的加密时间为0.021秒

最后是查询操作

执行如下指令，我们将查询结果保存在data/result目录下

1
python .\tenseal_matching.py -a BFV -i data/enc_matching_imgs -o data/result -c keys/private_context -db .\encrypted_images.db

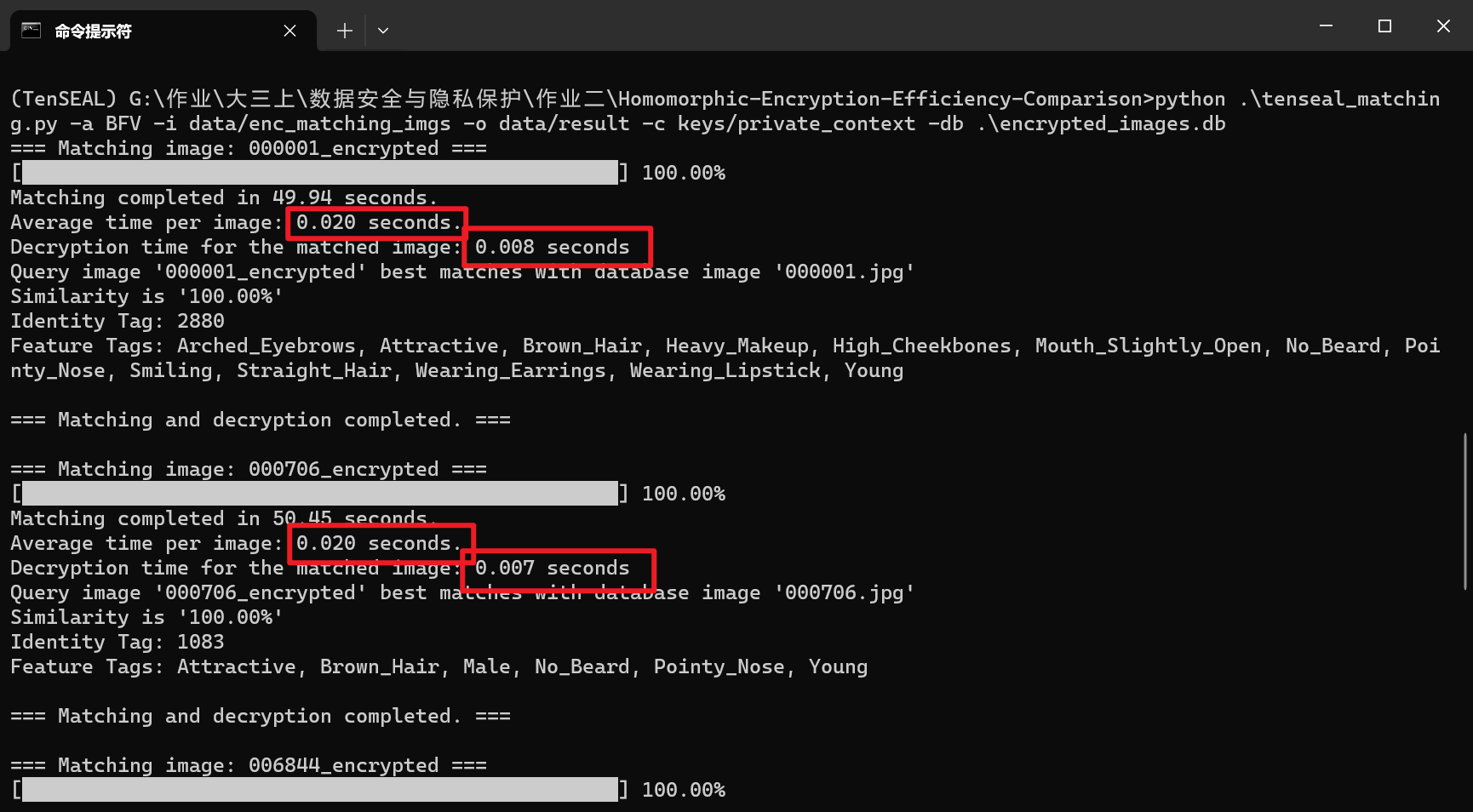
单张图片的匹配操作（即密态计算）时间为0.02秒，解密时间为0.007秒左右

我们的待匹配图像中有两张数据库中已有图像，以及三张数据库中未出现过的图像

数据库中存在的图片都成功匹配到相同图片

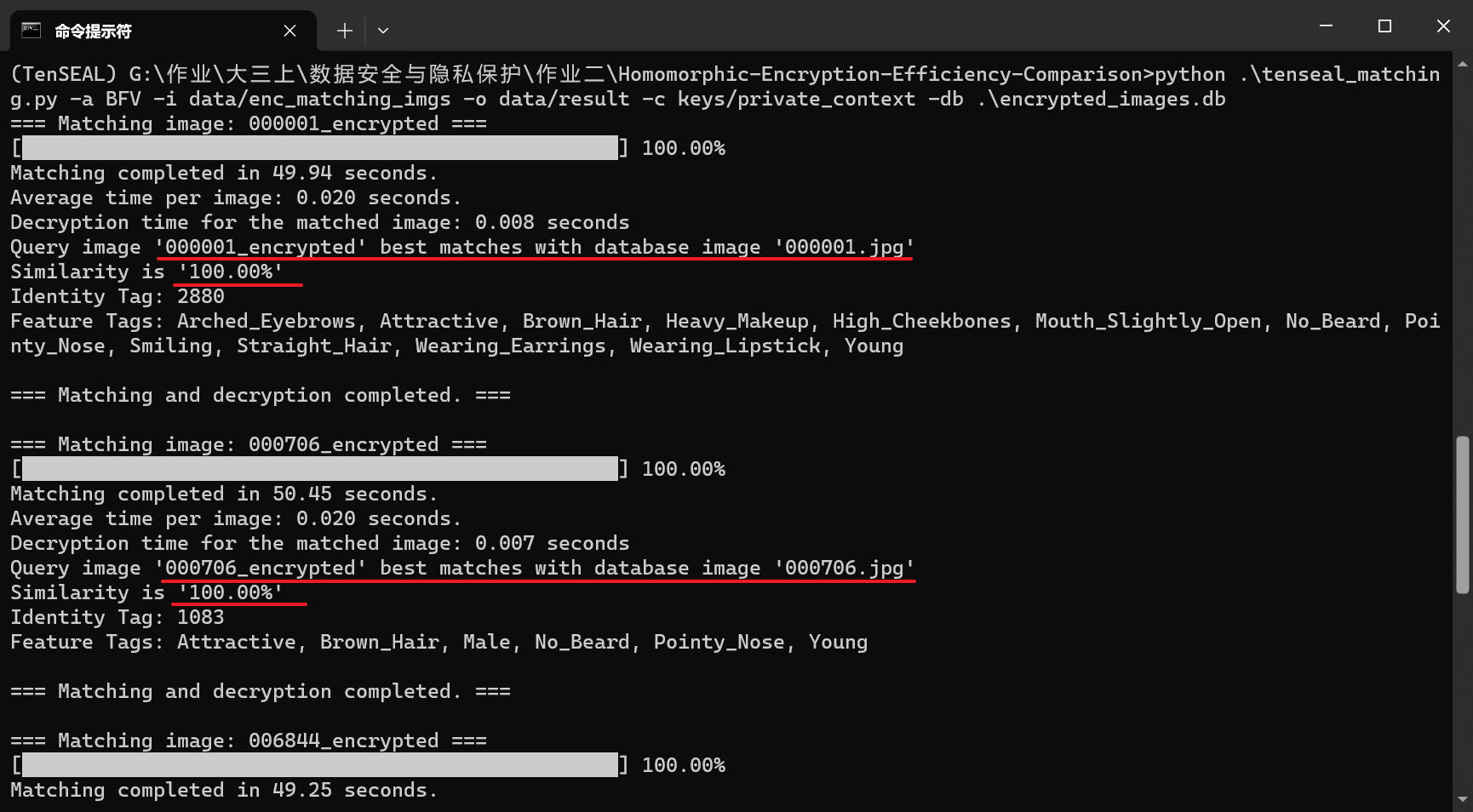
而不存在的图片则匹配到一个相似度较高的图

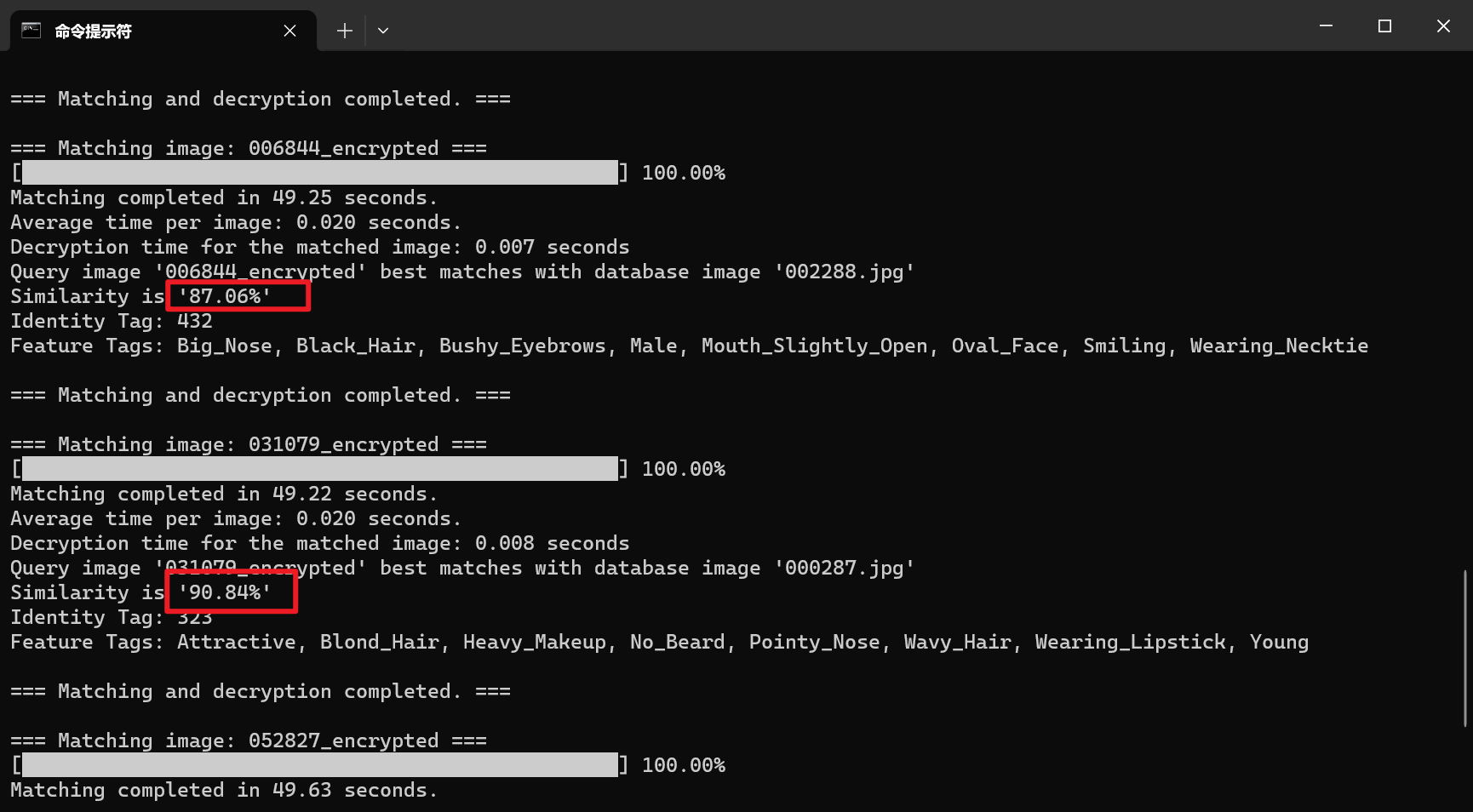
我们可以打开data/matching_imgs和data/result文件夹来对比结果的效果

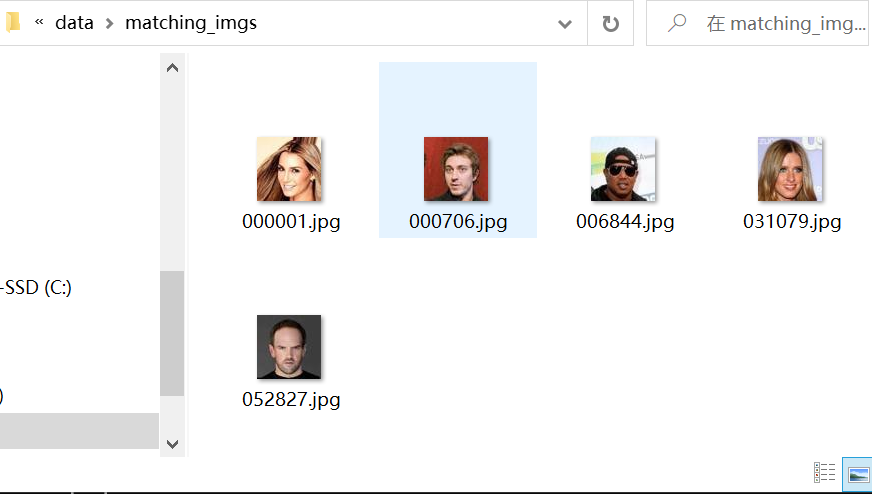
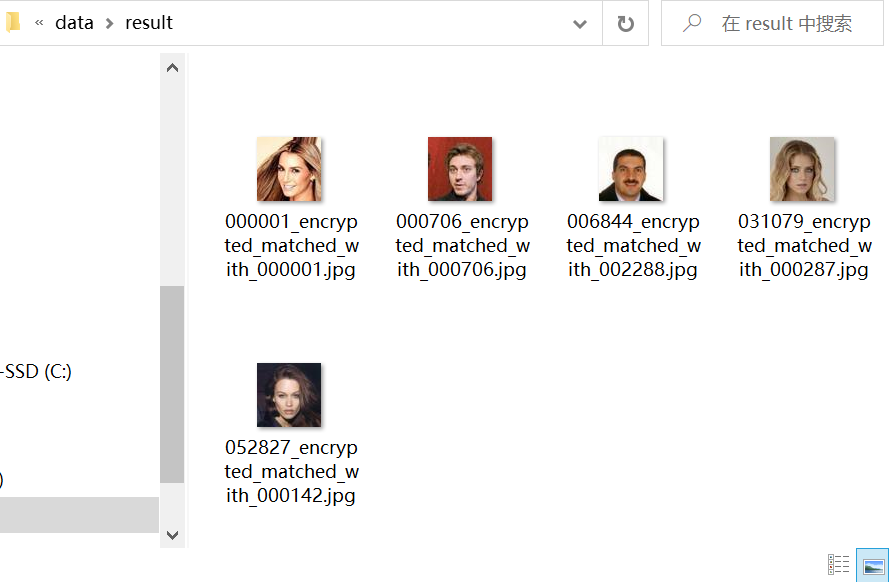
匹配到的图像与原图在人脸的位置以及发型上都较为相似，符合欧氏距离应有的匹配效果

CKKS

BFV的加密参数如下所示

1
global_scale = 2**40

依次运行以下指令

1
2
3
4
python tenseal_encrypt.py -a CKKS -i data/storage_imgs -o data/enc_storage_imgs
python .\DBuploader.py -i .\data\enc_storage_imgs\
python tenseal_encrypt.py -a CKKS -i data/matching_imgs -o data/enc_matching_imgs -c .\keys\public_context
python .\tenseal_matching.py -a CKKS -i data/enc_matching_imgs -o data/result -c keys/private_context -db .\encrypted_images.db

统计得到单张图像的加密时间为0.024秒左右

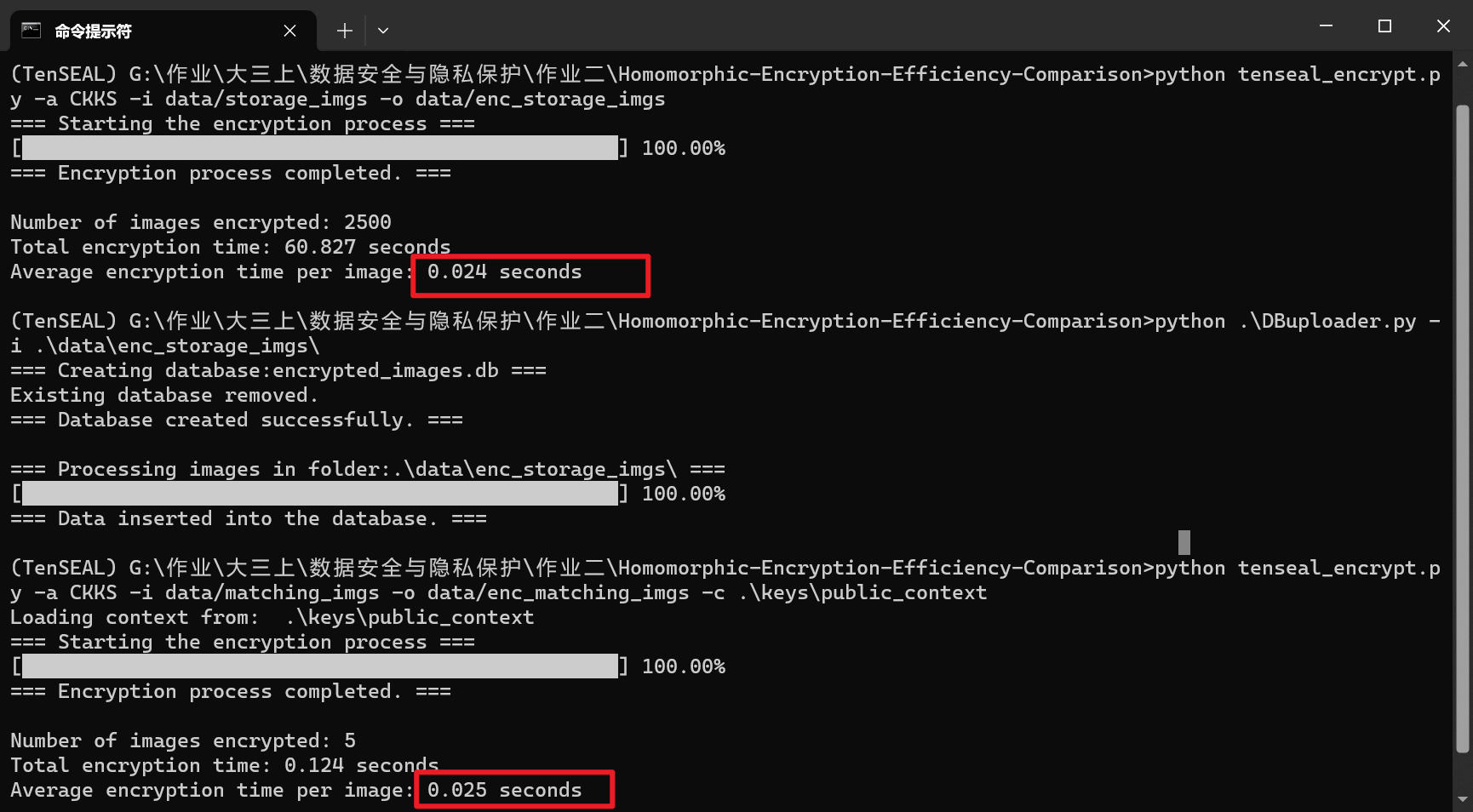
存储大小同样是2MB左右

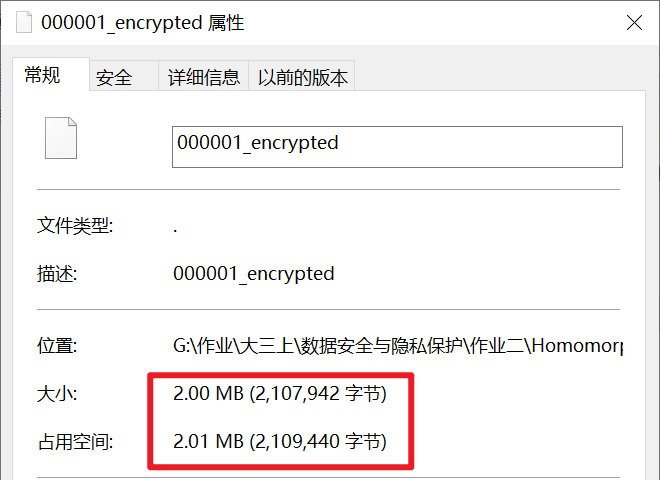
测试查询匹配

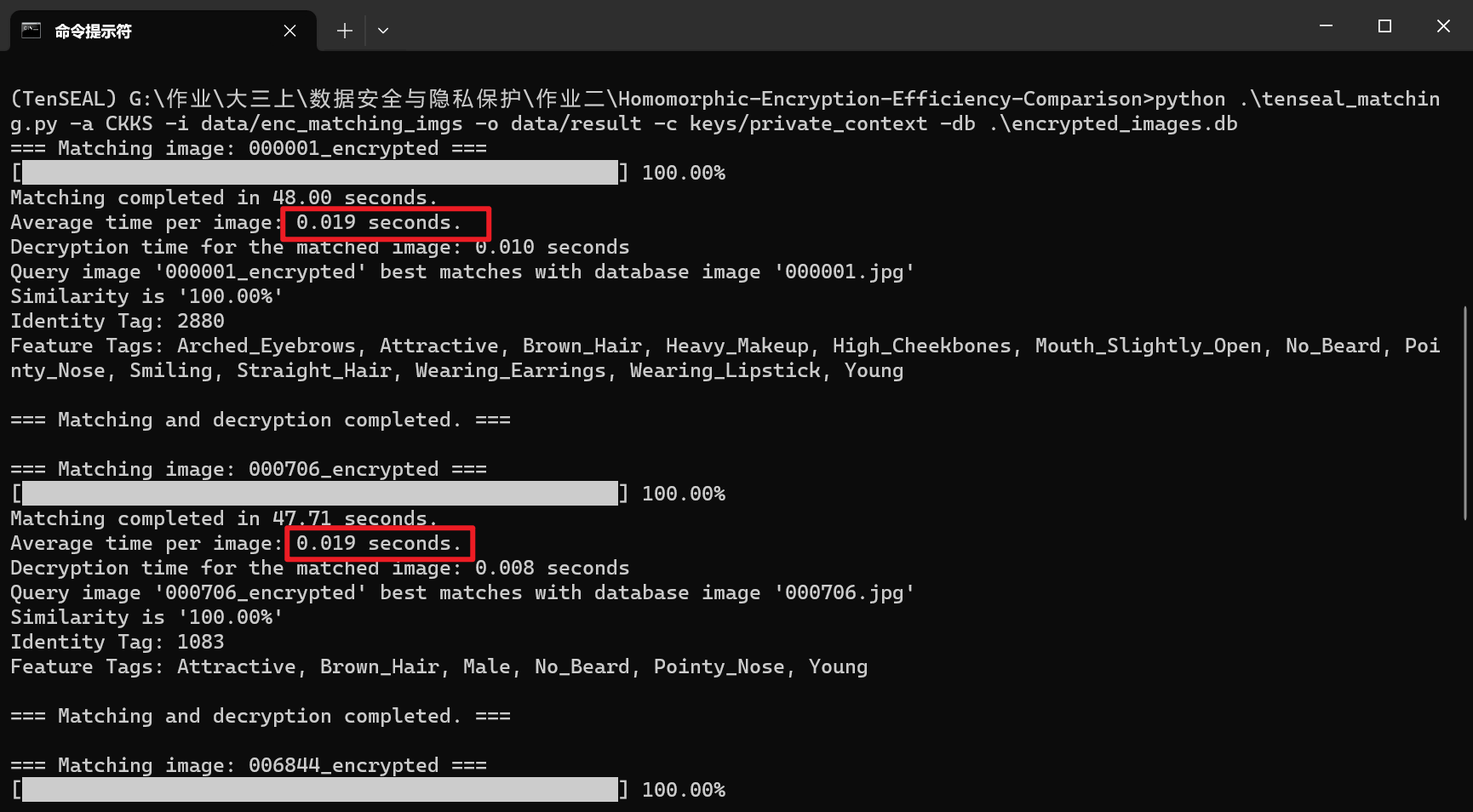
单张图片的匹配操作（即密态计算）时间为0.02秒，解密时间为0.008秒左右

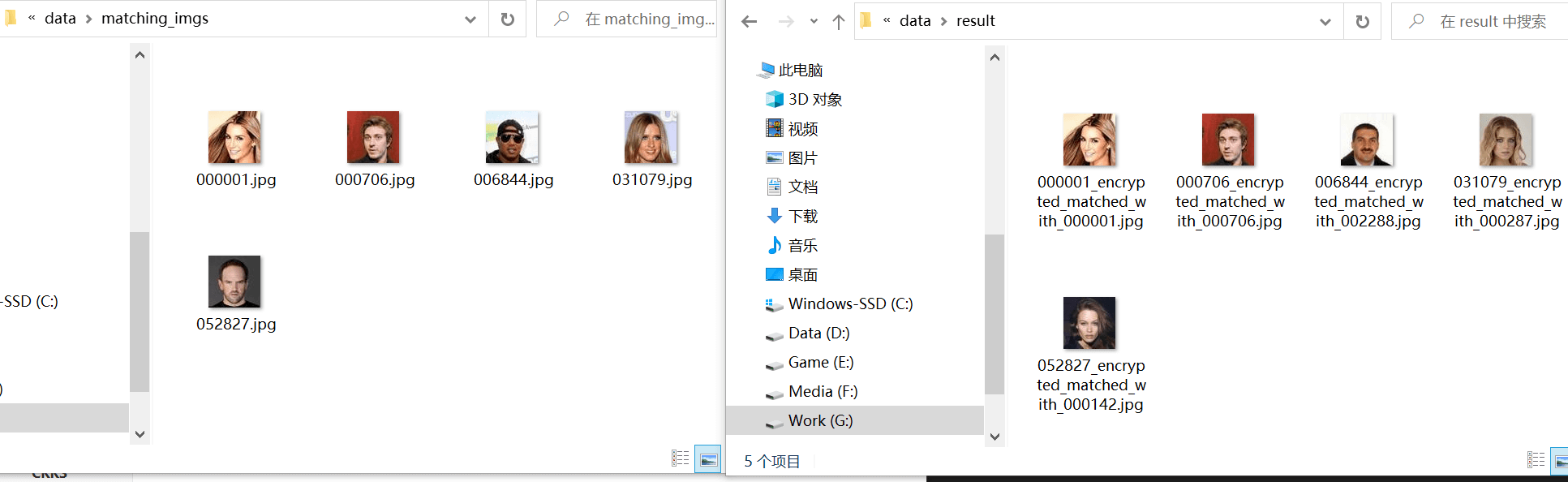
最后的识别结果和BFV一致

对比不同参数

将收集的数据列为更为直观的表格

算法 单张图像加密时间 单张加密图像大小 单张图像匹配时间 单张图像解密时间
BFV 0.019s 2MB 0.02s 0.007s
CKKS 0.024s 2MB 0.019s 0.008s

当参数设置相近时，BFV和CKKS算法在图像数据加密结果方面的效果相似，表明这两种算法在处理此类数据时具有一定的等效性。

而在加密花费的时间上，BFV相对于CKKS速度更快

造成这种现象的原因，可能是CKKS是运用在浮点级数据上的算法，对整数运算的支持程度并没有BFV高

我们将BFV的plain_modulus参数调大一些，设为786433

而CKKS的global_scale参数设为2**60

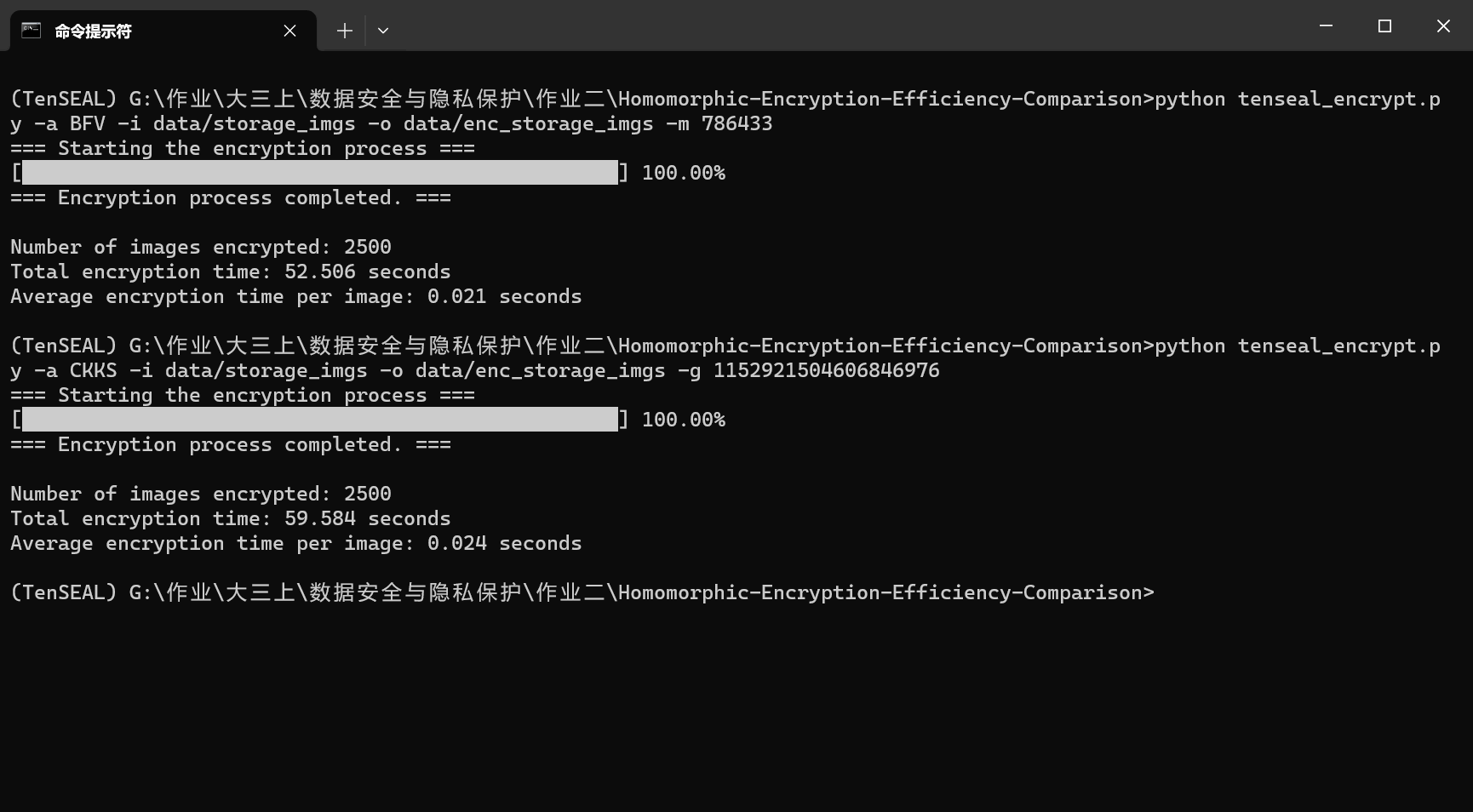
可以得到下表测试数据

算法 plain_modulus global_scale 单张图像加密时间
BFV 65537 0.019s
BFV 786433 0.021s
CKKS 2**40 0.024s
CKKS 2**60 0.024s

可以发现，当密文空间增大、加密安全性增加时，BFV的加密时间增长幅度更大

总的来说，BFV更适合需要精确整数计算的场景，而CKKS更适合于可以接受一定近似的浮点数计算。在加密的效率上，当数据量较大时，BFV比CKKS的效率更高，且CKKS对密文空间大小的敏感程度更高