前言

本系列文章为学校课程《数字图像处理》布置的一些小project作业

除了给出每个问题的解答和代码，我也会附上相关知识点，以方便后续复习

前置概念

图像复原

基本概念

图像复原的目的是针对质量降低或失真的图像，试图恢复其原始的内容或质量

获得使图像质量下降的先验知识，建立退化模型是图像复原处理的前提与关键

图像恢复总是假定已知或可以通过估计得到引起图像降质的模型，而图像增强不需要知道图像降质模型

图像退化与复原模型

引起图像质量下降的客观因素：

成象系统的象差、畸变、带宽有限等造成图像失真
几何失真：由于成象器件拍摄姿态和扫描非线性引起
灰度失真：光学系统或成象传感器本身特性不均匀，造成同样亮度景物成象灰度不同
运动模糊：成象传感器与被拍摄景物之间的相对运动，引起所成图像的运动模糊
辐射失真：由于场景能量传输通道中的介质特性如大气湍流效应、大气成分变化引起图像失真
噪声干扰：图像在成象、数字化、采集和处理过程中引入的噪声等

针对上述客观因素，建立图像退化模型，是进行图像复原处理的第一步

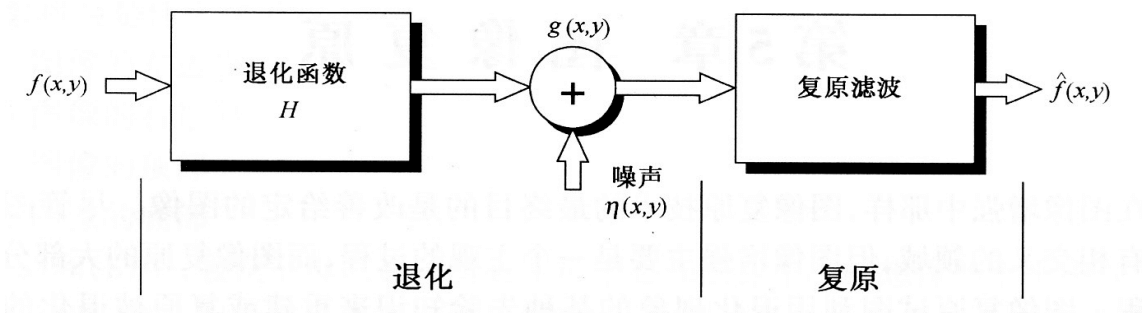
降质图像可表示为：$g(x, y) = H[f(x, y)] + \eta(x, y)$，其中 $H[\cdot]$ 是综合所有退化因素的函数

建立图像退化模型，即获得退化系统$H$和噪声$\eta$的模型

图像复原基本原理

图像复原的本质即沿着使图像降质的逆过程恢复图像本来面貌

实际的复原过程相当于设计一个滤波器，使其能从降质图像中计算得到真实图像的估值，使其根据预先规定的误差准则，最大程度地接近真实图像。

逆问题经常存在非唯一解，甚至无解。为了得到逆问题的有用解，需要有先验知识以及对解的附加约束条件

我们可以使用线性系统来近似退化过程，这样图像的退化可以看作原始图像与退化函数的卷积，因此线性图像复原往往被称为图像去卷积（反卷积），所采用的滤波器称之为去卷积滤波器

噪声模型

噪声模型及参数估计

下面是常见的噪声的概率密度函数图

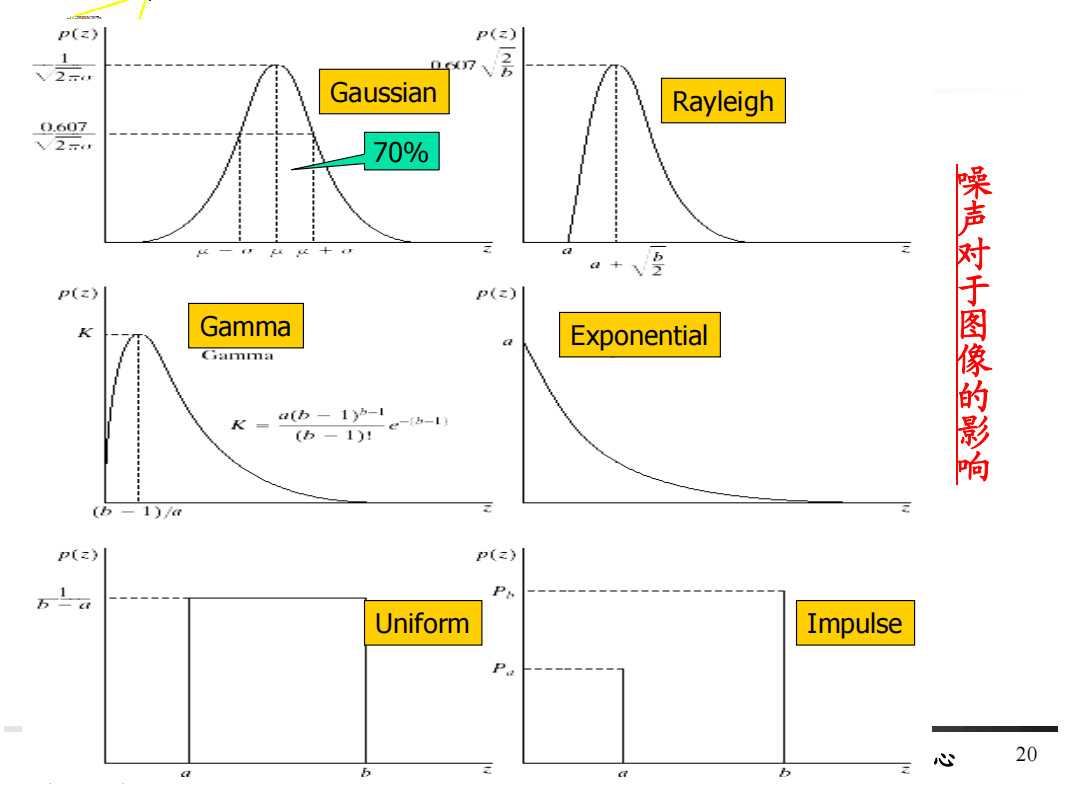
其中横轴$z$表示灰度值，而纵轴则表示该灰度值出现的概率

下图是不同噪声的效果比较

总的来说，我们想要建立一个噪声模型，关键是得到或估计其参数

对于Gaussian, uniform, Rayleigh, Erlang, exponential noises等噪声，关键是得到其均值与方差

$ \mu = \sum_{z_i \in S} z_i p(z_i) $

$\sigma^2 = \sum_{z_i \in S} (z_i - \mu)^2 p(z_i) $

而脉冲噪声（椒盐噪声）则类通过直方图获取参数$P_a$和$P_b$

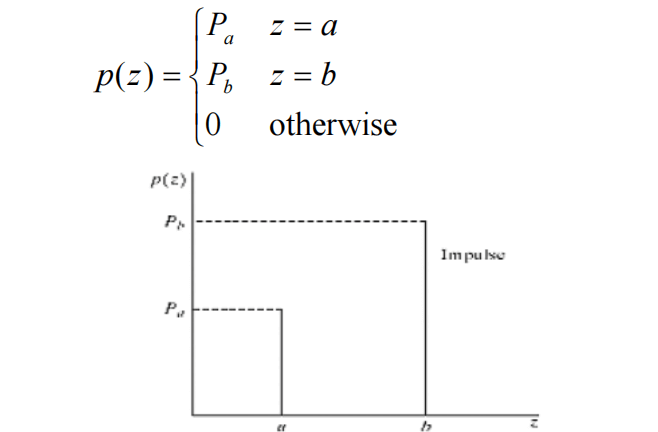
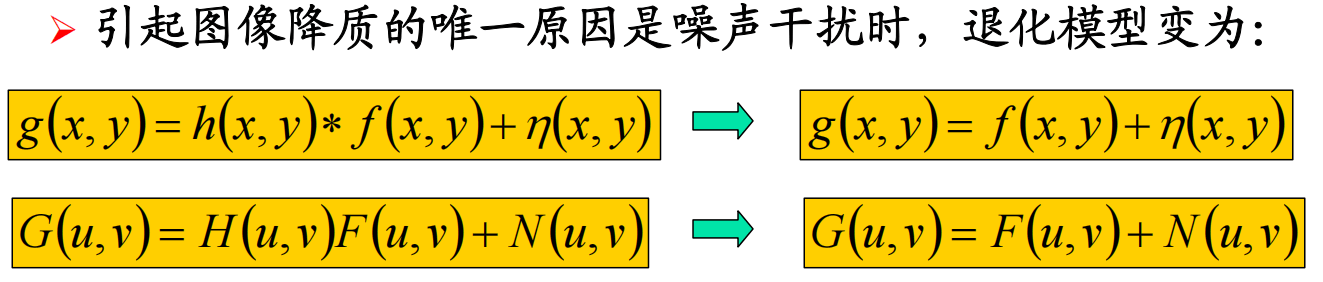
只存在噪声的复原

对于只存在噪声的图像的复原，我们通常选择空间滤波技术

固定滤波器

固定滤波器（Fixed Filters），也常被称为预定义滤波器或非自适应滤波器，是图像处理中一类预先定义好的滤波器，它们有固定的模板（kernel）或掩模（mask）。这些滤波器不会根据图像内容或其他外部信息改变其内核值

下面是一些常见的固定滤波器

算术均值滤波器 (Arithmetic Mean Filter):
$\hat{f}(x, y) = \frac{1}{mn} \sum_{(s,t) \in S_{xy}} g(s, t)$
$S_{xy}$ 是以像素$(x, y)$为中心的邻域集合。

$g(s, t)$ 是输入滤波器的图像在位置$(s, t)$的像素值。
几何均值滤波器 (Geometric Mean Filter):
- 非线性滤波
- 平滑度与算术滤波器相当
- 图像细节丢失更少
谐波均值滤波器 (Harmonic Mean Filter):
- 对“盐”噪声较好
- 不适用于“胡椒”噪声
- 善于处理高斯噪声

当然还有一类固定滤波器，它们基于像素的顺序统计特性决定其相应值

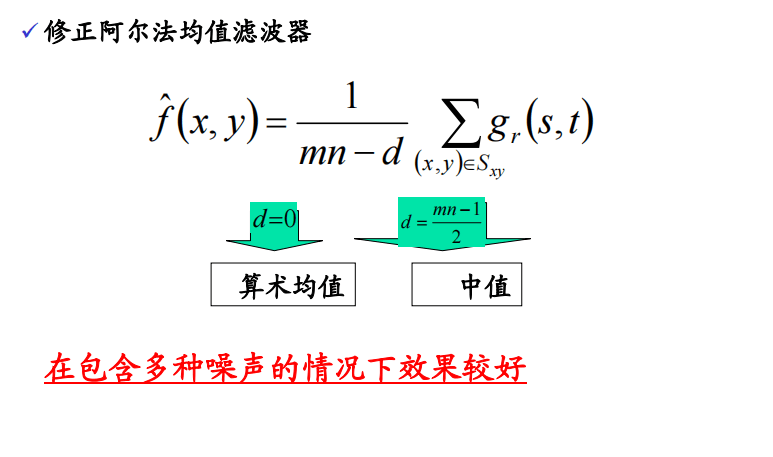
固定滤波器在图像恢复上存在一定的缺陷：

固定滤波器未考虑图像的局部特性，难以达到更好效果
为提高滤波性能，固定滤波器日益复杂，但适用面却日益缩小
滤波器窗口越大，图像细节丢失越严重
通常须在保存图像细节与噪声滤除之间寻求某种折衷

自适应滤波器

自适应滤波器很好的解决了固定滤波器的问题

通过结合图像的局部特性，它能自动修改滤波器参数或滤波策略

除了以均值和方差建立的自适应模型，还有如下的自适应中值滤波器

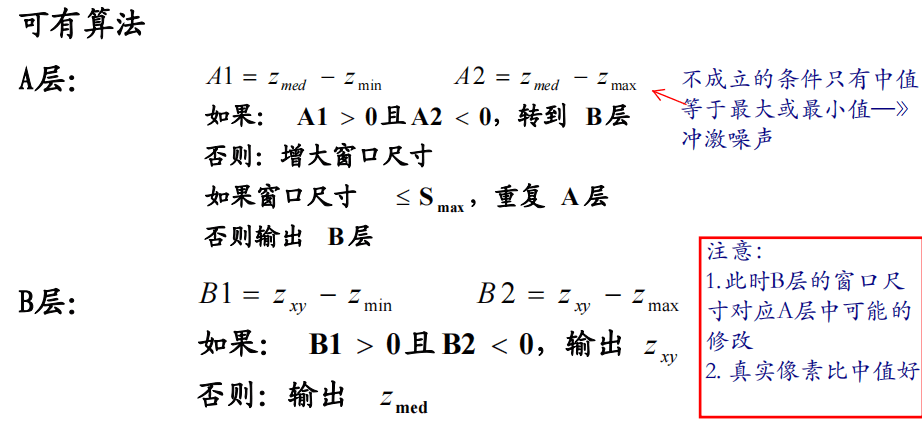
频域滤波降低周期噪声

常用的频域滤波有两种：带阻滤波器和陷波滤波器

带阻滤波器（Band-stop Filter）

带阻滤波器设计用来抑制一定频率范围内的信号，同时允许其他频率的信号通过。它在频域中形成一个“带阻”区域，这个区域对应于周期性噪声的主要频率成分。

应用场景：当周期性噪声的频率集中在一个较宽的频率范围内时，带阻滤波器特别有效。
设计考虑：需要确定噪声频率的上下界，并据此设计滤波器。
效果：能够同时抑制多个相近的周期性噪声频率。

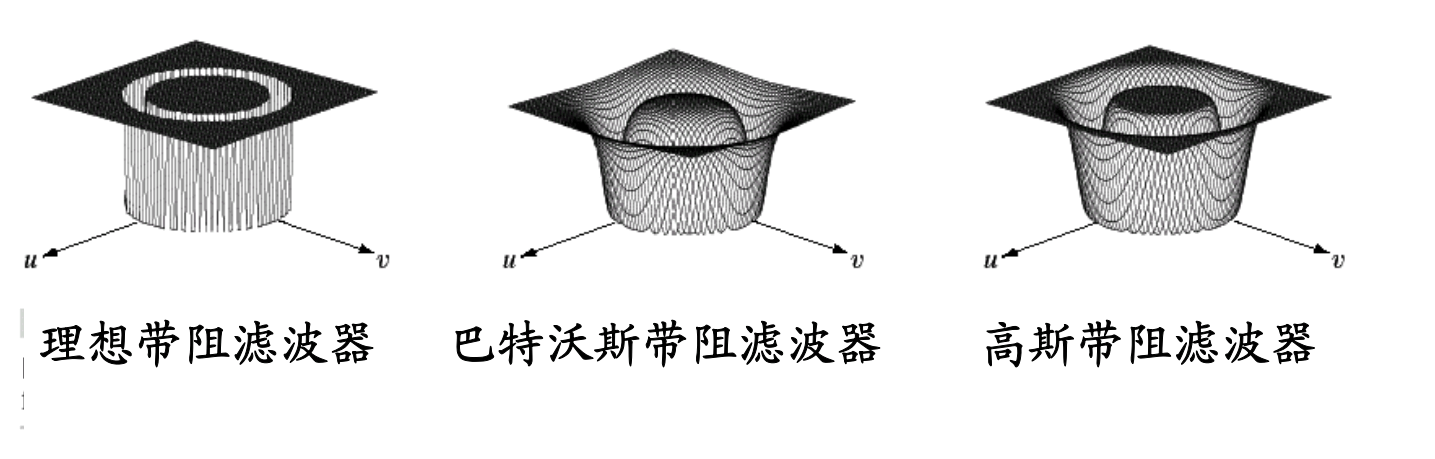
一个带阻滤波效果的例子如下

陷波滤波器（Notch Filter）

陷波滤波器是一种更加精确的滤波方式，它旨在抑制一个或几个特定的频率点，而对其他频率的信号影响较小。这种滤波器在频域中形成一个或多个“陷阱”，精确地消除特定频率的噪声。

应用场景：当周期性噪声集中在一个或几个非常特定的频率点上时。
设计考虑：需要精确知道噪声的频率，并在这些频率点上设计陷波。
效果：非常精确地消除特定频率的噪声，对其他频率成分的影响很小。

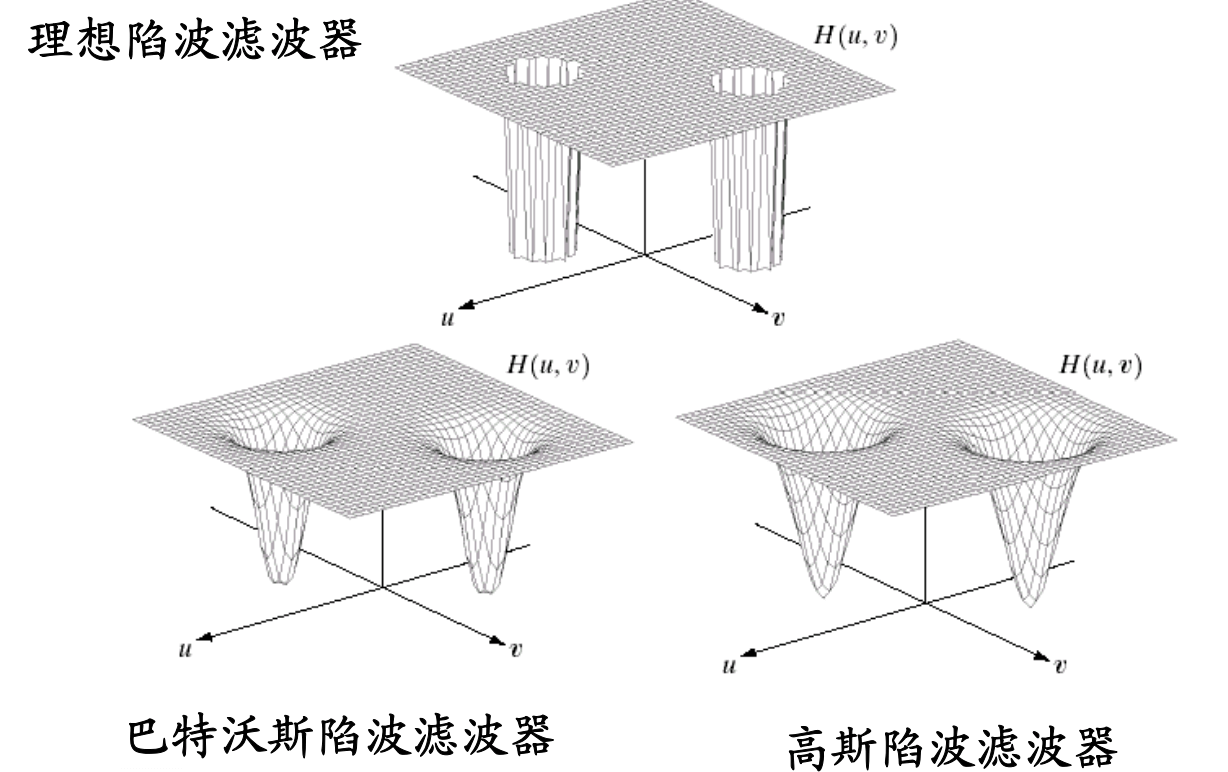
注意上图中右上角为噪声的频域图像，我们需要消除它则需要纵轴上的陷波滤波器

系统退化

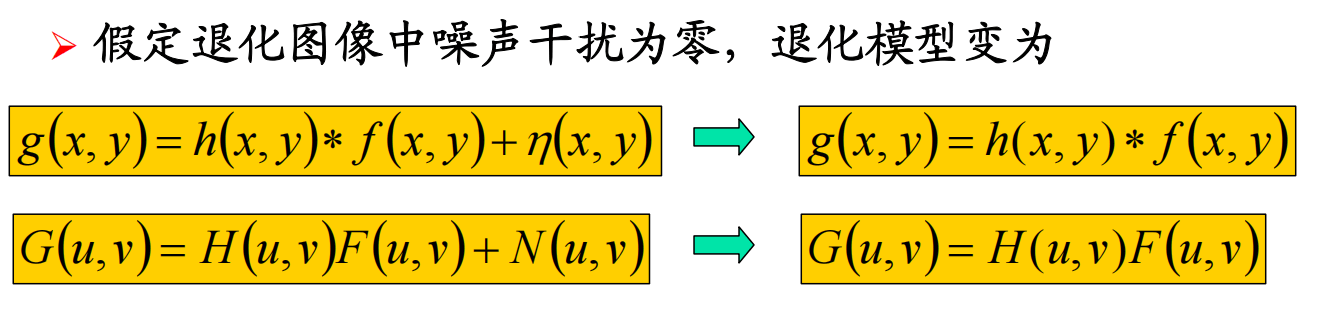
估计退化函数

对退化函数$H(u,v)$的估计过程常称为系统辨识过程

图像观察估计法

选择图像中具有强信号与强特征的局部区域图像$g_s(x,y)$，设法构建一个具有相同大小与特征、但没有退化

的近似图像，可有$H_s(u,v) = \frac{G_s(u,v)}{\hat{F}_s(u,v)}$

试验估计法

使用或设计一个与图像退化过程相似的装置（过程），使其成像一个脉冲，可得到退化系统的冲激响应

$H(u,v) = \frac{G(u,v)}{A}$

模型估计法

从引起图像退化的基本原理进行推导，进而对原始图像进行模拟，在模拟过程中调整模型参数以获得尽可能精确的退化模型

常见的模型有下面几种

大气湍流模型：$H(u,v) = \exp \left[ -c (u^2 + v^2)^{\frac{5}{6}} \right]$

大气扰动模型：$h(i,j) = K \cdot \exp \left( -\frac{i^2 + j^2}{2 \sigma^2} \right)$

运动模糊模型：$H(u,v) = \frac{T}{\pi (ua + vb)} \sin \left[ \pi (ua + vb) \right] e^{-j \pi (ua + vb)}$

光学散焦模型：$H(u,v) = \frac{J_1(\pi d \rho)}{\pi d \rho} \ \rho = (u^2 + v^2)^{\frac{1}{2}}$

想要进行模型估计，可以采取点扩展函数法

点扩展函数法的思想就是将退化函数看作将一个点光源（或不同频率的光源）输入成像系统，输出则是相应的PSF(或PSF的傅里叶变换函数)

逆滤波

但是这周自己哦空额的逆滤波存在一个问题

$F(u,v) = \frac{G(u,v)}{H(u,v)}-\frac{N(u,v)}{H(u,v)}$

当$H(u,v)$等于零或非常小的数值点上，噪声的影响会大大增强

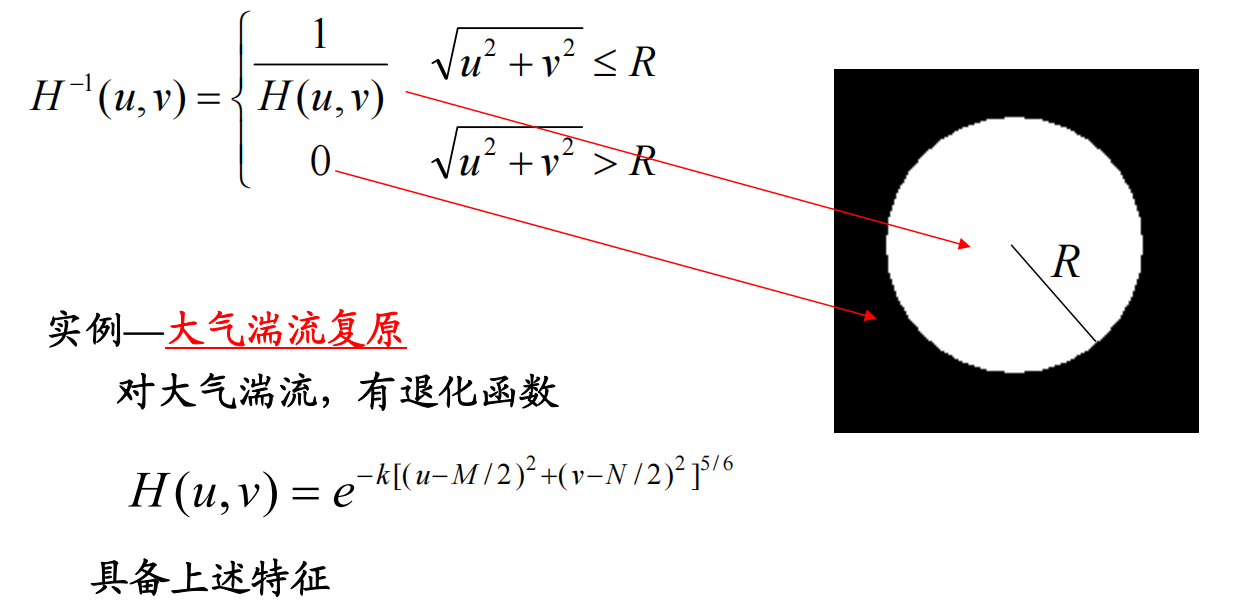
一种改进方法是伪逆滤波复原

通过对$H(u,v)$规定一个门限值

$H^{-1}(u,v) =
\begin{cases}
\frac{1}{H(u,v)}, & |H(u,v)| > \delta \
0, & |H(u,v)| \leq \delta
\end{cases}$

当我们针对特定噪声进行逆滤波，例如高斯白噪声

那么$H(u,v)$可能在很高的频率时趋于零

此时我们只需对伪逆滤波施加圆形范围限制即可

最小均方误差滤波（维纳滤波）

维纳滤波假设图像和噪声均属于随机信号（平稳随机过程），且相互之间互不相关

而目标是寻找最佳复原图像，使得均方误差最小

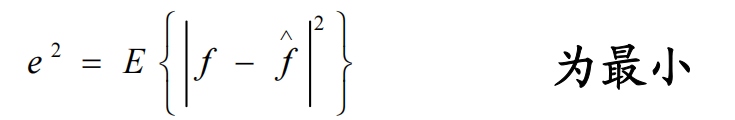
维纳滤波的结果如下

$\hat{F}(u,v) = \frac{\left| H(u,v) \right|^2}{\left| H(u,v) \right|^2 + S_n(u,v)/S_f(u,v)} \cdot \frac{G(u,v)}{H(u,v)}$

不过值得注意的是，维纳滤波器建立在最小化统计准则基础上，只是在平均

意义上最优

HW 图像退化与复原

作业要求：

使用教科书中的方程（5.6-11）实现一个模糊滤镜，并用参数 a=b=0.1 和 T=1 对测试图像 ‘book_cover.jpg’ 进行模糊处理。（20%）

向模糊图像添加均值为0、方差为500的高斯噪声。（10%）

使用逆滤波恢复模糊图像和模糊噪声图像。（30%）

使用至少3个不同参数的参数化维纳滤波恢复模糊噪声图像，并与3的结果进行比较和分析。（40%）

原图如下

book_cover

在开始任务之前，考虑到后续生成的中间图像的像素值范围可能超过$[0,255]$，我们需要定义一个归一化函数，方便后续归一化并保存中间图像

function result = normalize_image(image)
    result = image - min(image(:)); % 将图像平移到最小值为0
    result = result / max(result(:)); % 缩放图像使最大值为1
    result = uint8(result * 255); % 转换为0-255的uint8图像
end

图像模糊

首先完成第一个任务

教科书中的5.6-11方程为图像运动模糊模型

$H(u,v) = \frac{T}{\pi (ua + vb)} \sin \left[ \pi (ua + vb) \right] e^{-j \pi (ua + vb)}$

首先我们读取图像，并将其转到频率域

I = imread('book_cover.jpg');
[M,N] = size(I);
I = double(I);  
F = fftshift(fft2(I));

由于后续有较为复杂的操作，我们需要使用double()将I变为实数矩阵

我们按照题目定义运动模糊模型的参数

1
2
3

a = 0.1;
b = 0.1;
T = 1;

接下来我们就可以定义运动模糊模型的退化函数了

H = zeros(M,N);
for u = 1:M
    for v = 1:N
        x = pi * ((u-M/2)*a + (v-N/2)*b); 
        if x == 0
            H(u,v) = T;
        else
            H(u,v) = (T / x) * sin(x) * exp(-1i*x);
        end
    end
end

当然，我们需要额外增加判断，避免退化函数中pi * ((u-M/2)*a + (v-N/2)*b这一部分太小，导致比值趋近于无穷大，当x为0时，我们应该将H设为一个有限值

我们将退化函数与原图的频域相乘，进行模糊处理

1
2
3

G = H .* F;
blurred_image = normalize_image(abs(ifft2(G)));
imwrite(blurred_image, './result/blurred_image.png');

注意在最后需要对空域的模糊图像进行归一化

得到下图结果

blurred_image

可以发现非常接近现实生活中因为物体运动而产生的模糊图片

添加噪声

第二个任务是向模糊图像添加高斯噪声，这样可以得到完整的退化模型

首先我们根据题目的要求，生成一个均值为0、方差为500的高斯噪声

1 2	noise = randn(M,N) * sqrt(500); Fn = fftshift(fft2(noise));

将噪声与模糊图像相加，得到模糊噪声图像

1
2
3

Gn = G + Fn;
blurred_noisy_image = normalize_image(abs(ifft2(Gn)));
imwrite(blurred_noisy_image, './result/blurred_noisy_image.png');

blurred_noisy_image

我们可以将原图和两张生成的退化图像进行对比

逆滤波复原

将模糊图像和模糊噪声图像分别除以退化函数，得到复原后的图像

% 逆滤波恢复模糊噪声图像
F_hat1 = G ./ H;
F_hat1(isnan(F_hat1)) = 0; 
F_hat1(isinf(F_hat1)) = 0; 
inverse_filtered_image = normalize_image(abs(ifft2(F_hat1)));
imwrite(inverse_filtered_image, './result/inverse_filtered_image.png');

% 逆滤波恢复模糊噪声图像
F_hat2 = Gn ./ H;
F_hat2(isnan(F_hat2)) = 0; 
F_hat2(isinf(F_hat2)) = 0; 
inverse_filtered_noisy_image = normalize_image(abs(ifft2(F_hat2)));
imwrite(inverse_filtered_noisy_image, './result/inverse_filtered_noisy_image.png');

下图是模糊图像的逆滤波复原图

inverse_filtered_image

可以发现和原图基本一致

而下图是模糊噪声图像的逆滤波复原图

inverse_filtered_noisy_image

可以发现比原来的噪声强度还大

我们可以从逆滤波的公式中找到原因

$F(u,v) = \frac{G(u,v)}{H(u,v)}-\frac{N(u,v)}{H(u,v)}$

对于仅仅模糊的图像（不含噪声），如果已知确切的模糊函数，逆滤波可以恢复得到原始图像

而当存在噪声时，由于噪声通常具有高频成分，在逆滤波的过程中，除以模糊核的频率响应会放大这些高频成分，导致噪声也被显著放大

维纳滤波

我们定义三个维纳滤波参数K = [0.01, 0.1, 1]

根据这三个参数分别得到维纳滤波的复原图像

F_wnr = zeros(M,N,length(K));
for k = 1:length(K)
    F_wnr(:,:,k) = conj(H) ./ (abs(H).^2 + K(k)) .* Gn;
    F_wnr(:,:,k) = ifftshift(F_wnr(:,:,k));
    F_wnr(:,:,k) = ifft2(F_wnr(:,:,k));
end