数字图像处理 作业三
前言
本系列文章为学校课程《数字图像处理》布置的一些小project作业
除了给出每个问题的解答和代码,我也会附上相关知识点,以方便后续复习
前置概念
空间域滤波回顾
空间域滤波也叫模板,主要涉及相关和卷积两种基本运算
- 相关运算:将模板当权重矩阵作加权平均;
- 卷积运算:模板先沿纵轴翻转,再沿横轴翻转后再加权平均。
如果模板是对称的,那么相关与卷积运算结果完全相同
领域运算实际上就是卷积和相关运算,用信号分析的观点就是滤波
利用空间域的图像平滑,可以阻截高频的噪声信号,但是往往图像的边缘部分(细节)也处于高频部分
常见的滤波器有领域平均滤波、高斯滤波和中值滤波
空间域滤波本质上是个领域运算,且需要一个模板(阶为奇数的矩阵)
频域滤波
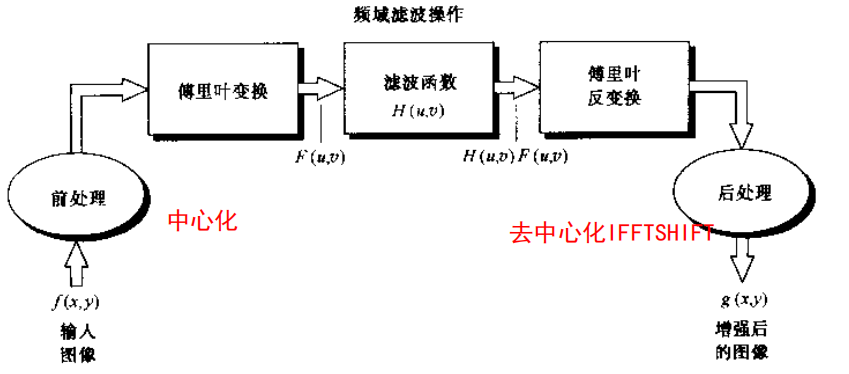
频域进行滤波操作相当于空间域做卷积操作
$f(x,y) * h(x,y) \Rightarrow F(u,v)H(u,v)$
空间域和频域的滤波器构成傅里叶变换对
$h(x,y) \Leftrightarrow H(u,v)$
从定义上来讲,频域滤波就是将信号中特定波段频率滤除的操作
所以,低通滤波就是是低频通过而使高频衰减的滤波器,高通滤波则相反
在滤波器模板规模较大时,频域内进行滤波计算更为有效,空间域的滤波器更适用于小规模模板。因为频域计算存在高效计算方法,如快速傅里叶变换可以将计算复杂度从$O(N^2)$下降到了$O(NlogN)$
滤波器间的关系
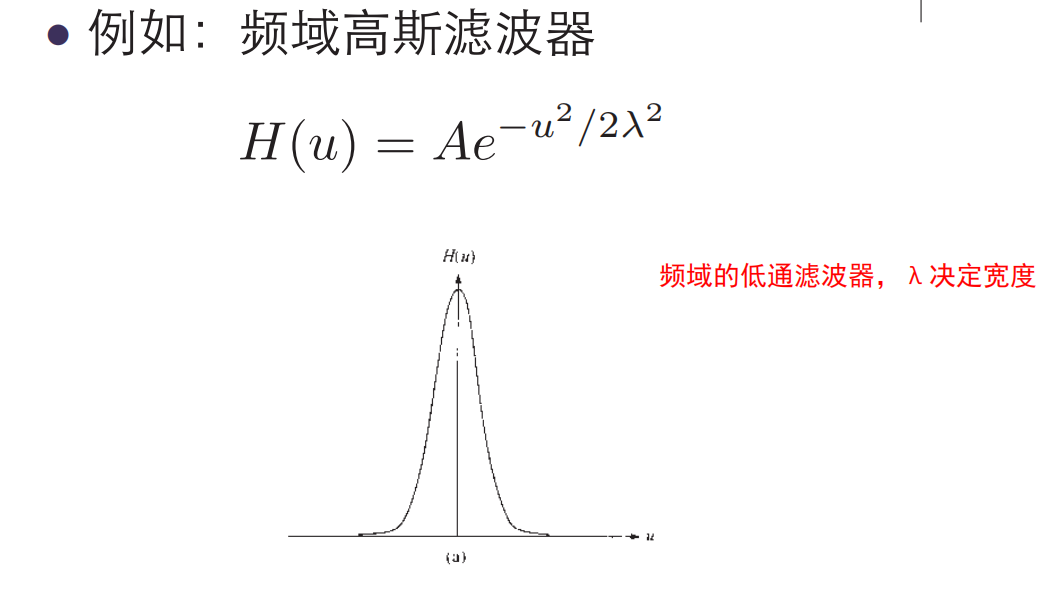
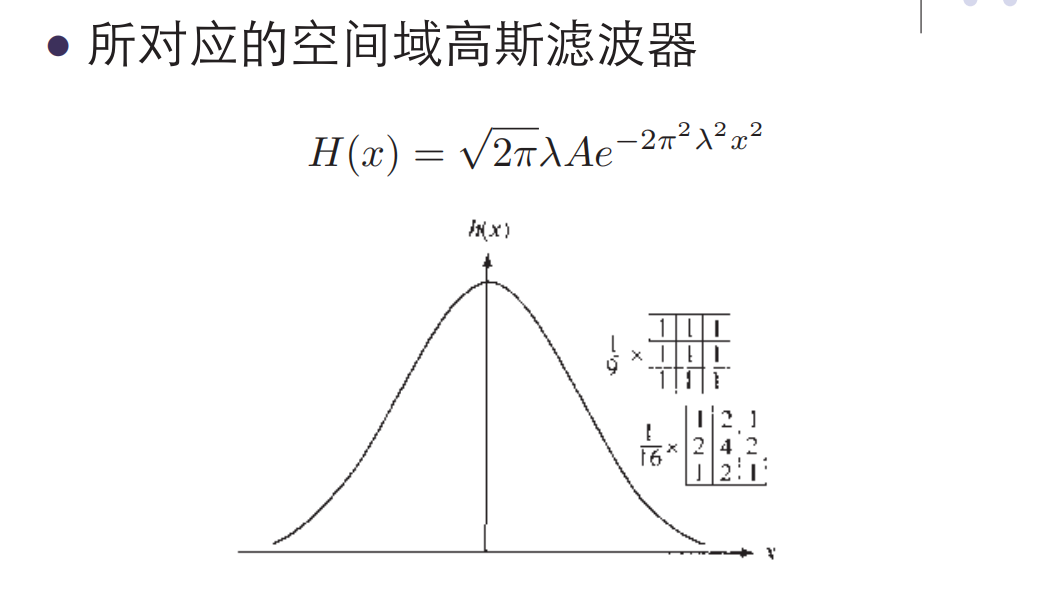
$H(u)$和$h(x)$构成傅里叶变换对
当$\lambda $很大时,$H(u)$变宽,$h(x)$变窄;当$\lambda $趋于无穷时,$H(u)$趋于常数函数,而$h(x)$则趋于一个冲激函数
另一个例子是带通滤波器
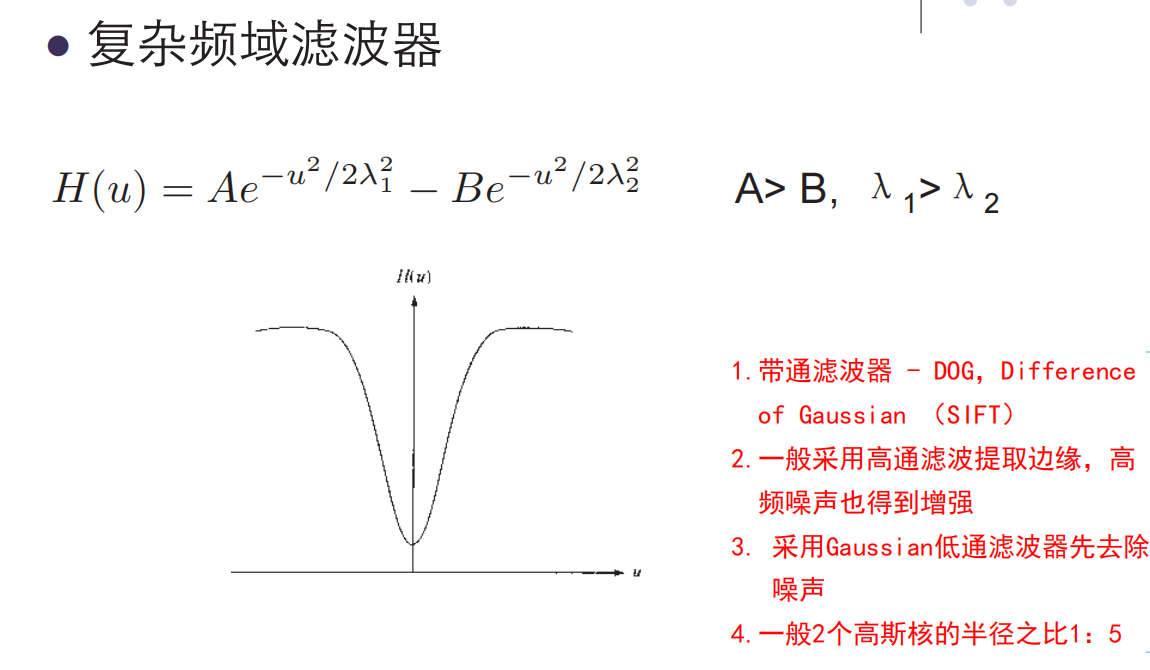
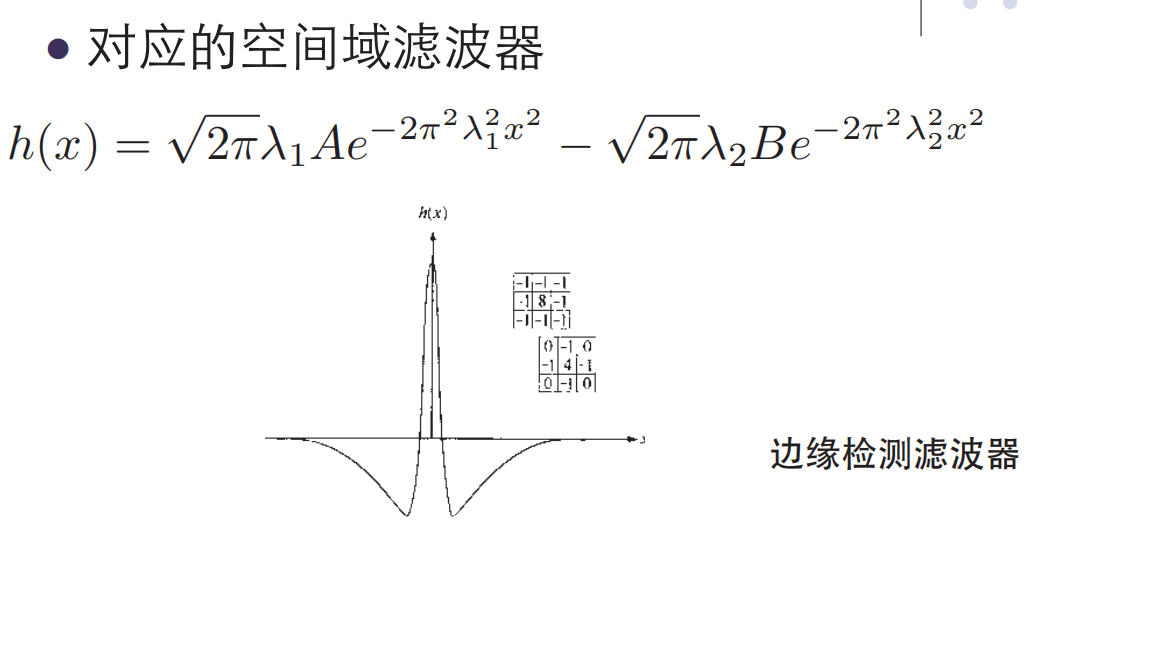
低通滤波
目的:低通滤波通过对频域上一定范围的高频分量进行衰减以达到平滑化,来增强图像
常见的低通滤波器有三种

应用:印刷和出版业的预处理功能、美容处理(减少人脸皮肤细纹)
理想低通滤波器(ILPF)
思想:截断傅里叶变换中所有高频成分
定义:以$D_0$为半径的圆内所有频率分量无损的通过,圆外的所有频率分量完全衰减
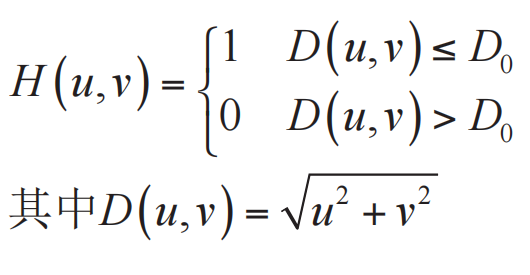
下面是一些实例
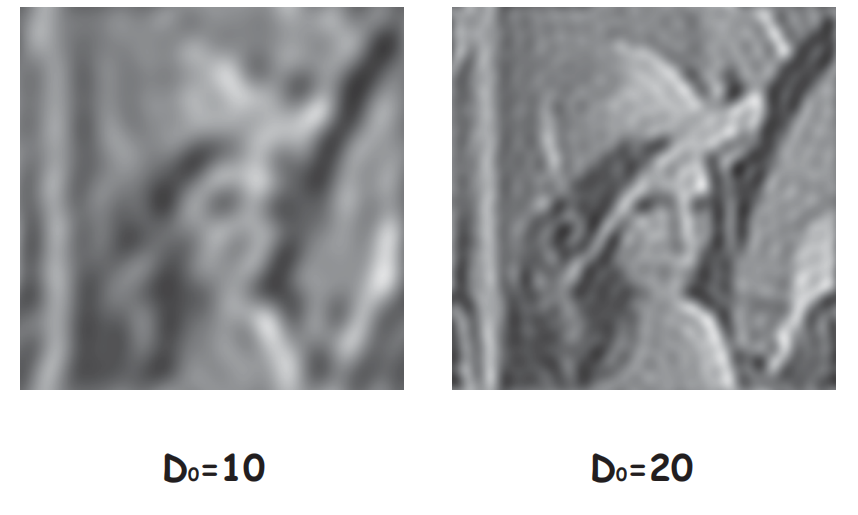


我们可以观察到理想低通滤波器存在的一些问题
模糊
对于带高斯噪声的lenna图像,虽然半径为5时包含了90%的能量,但严重的模糊表明图片的大部分边缘信息包含在滤波器滤去的10%能量之中
之所以$D_0$较高时,图像越模糊,我们可以结合空间域来理解:频域的滤波越窄,空域滤波越宽,即空域滤波时模板的尺寸越大
振铃
由于理想低通滤波在截止频率$D_0$附近对频谱过于粗暴的截断,导致对应空域滤波的图像外围会有一圈环形/多个环相互干扰,导致了振铃现象
总而言之,理想低通滤波器并不实用,
但这也给出了设计方向:需要尽量减少振铃或没有振铃,以及减少模糊
巴特沃思低通滤波器(BLPF)
思想:平滑的理想低通滤波器

相对于ILPF,BLPF的一个显著优点是在通过的频率与被滤掉的频率之间没有明显的截断
当阶数为1时,没有振铃现象
但是当阶数逐渐增高时,振铃现象会越来越明显,当阶数趋于无穷大时,BLPF=ILPF
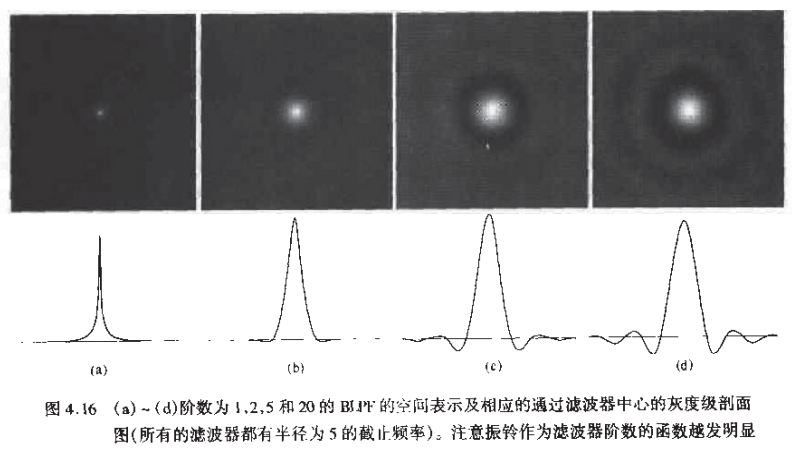
而另一个优点是,当和ILPF采用相同的$D_0$时,BLPF可以保留更多高频成分
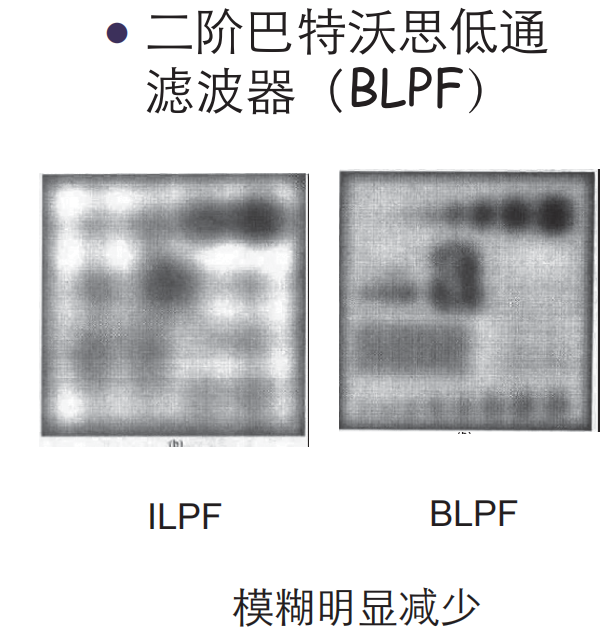
可以说,BLPF是一种在有效低通滤波和可接受的振铃特性之间的折中方案
高斯低通滤波器(GLPF)
思想:彻底没有振铃现象
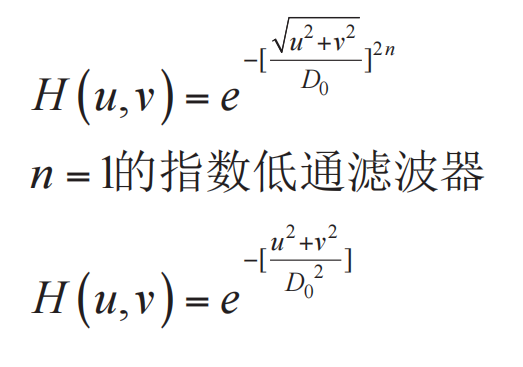
由于高斯滤波器的傅里叶反变换还是高斯,空域核没有震荡,所以不会产生振铃
高通滤波
目的:高通滤波的效果通常是使模糊图像变得清晰,即图像锐化处理
但是,高通滤波在增强细节的前提下,也增加了图片中的噪声能量。所以高通滤波器所处理的图像需要有较高的信噪比,否则图像锐化后,图像信噪比会更低
常见的高通滤波器有以下几种

理想高通滤波器(IHPF)
思想:截断傅里叶变换中所有低频成分
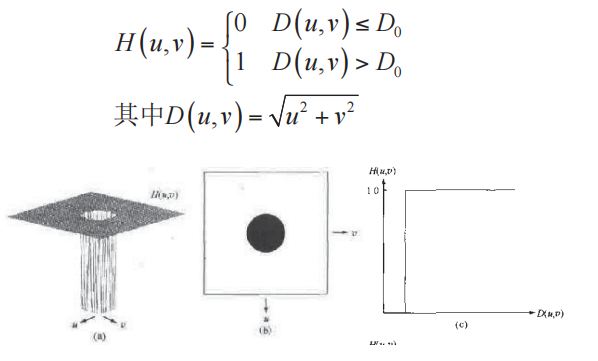
与理想低通滤波器类似,理想高通滤波器也存在振铃现象

巴特沃思高通滤波器(BHPF)
思想:平滑理想高通滤波器

高斯高通滤波器(GHPF)
思想:彻底消除振铃现象
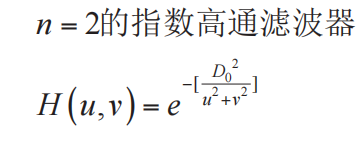
与GLPF性质类似的,GHPF比BHPF要稍微模糊,但彻底没有振铃现象

高斯差分滤波器(DoG)
思想:高斯滤波器的推广版。引入更多参数,用于解决更具体的实际问题

同态滤波
正常图像是在均匀光强度情况下获得的图像,实际上光照射是不均匀的,或者光强范围动态太大
同态滤波就是用于解决光照不均匀的影响

同态滤波的基本思想是通过对数变换将光照的影响转换为传统噪声模型进行处理
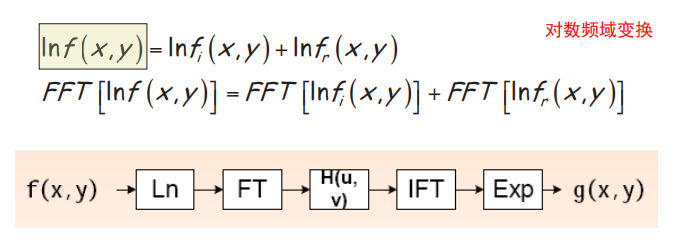
一般来说,光照的频率集中分布在低频部分
而反射到眼睛的图像种包含景物的各种信息,频率集中在高频分量
我们可以选择一种滤波函数,增强高频的贡献,减少低频的贡献

HW1 巴特沃思低通滤波器
作业要求:
给定图像barb.png,利用一阶Butterworth低通滤波器进行频域滤波,当 $D_0$ = 10, 20, 40,80 时,给出相应滤波图像,并分别以频域和空域的观点解释有关滤波结果。
提示:
(1)以 $(- 1)^{(x+y)}$ 乘以输入图像进行中心变换;
(2)直接以FFT2进行傅立叶变换;
(3)DFT反变换后取实部;
(4)以乘以(3)中结果,反中心变换。
由于图像频域的原点不在正中央,无法直接用滤波器处理,所以我们需要对图像先进行中心变换
将频域的坐标原点从(0,0)移至中心,我们只需要将原图乘以 $(- 1)^{(x+y)}$后再进行傅里叶变换
1 | for x = 1:rows |
巴特沃思公式如下

我们根据公式创建$H(u,v)$
1 | H = zeros(rows, cols); |
我们对频域图像进行滤波操作后再傅里叶逆变换得到空域图像
1 | filtered_img_fft = img_fft .* H; |
最后我们需要将图片反中心变换回来
1 | for x = 1:rows |
最后保存生成的滤波图片及对比图即可
1 | subplot(2, 3, i+1), imshow(uint8(img_filtered)), title(['D0 = ', num2str(D0)]); |
运行程序,我们可以得到如下结果

观察结果,我们可以发现,低通滤波器使得图像变得模糊,而随着增加,图像逐渐变得清晰
从频域来讲,低通滤波器在频域中的作用是允许低频分量通过,同时削弱或阻止高频分量。在图像处理中,高频分量通常对应于图像的边缘和细节部分,而低频分量则对应于图像的平滑区域。所以低通滤波器会使得图像的细节损失,变得平滑,或者说变得模糊。
当 增加时,更多的高频分量被允许通过。这意味着更多的细节和边缘信息被保留在图像中,因此图像变得更加清晰。
而从空域来讲,低通滤波可以看作是图像与一个平滑核的卷积。这个过程相当于”平均”图像中的像素值,使得图像变得平滑,也就是更加模糊。
当增加时,根据巴特沃思低通滤波器的公式,频域的滤波变宽,空域滤波变窄,即空域滤波时模板的尺寸变小,此时图像平滑程度减弱,拥有更多细节信息。
HW2 同态滤波器
作业要求:
采用同态滤波来增强图像‘office.jpg’细节,对数频域滤波器为:
$H(u,v) = (\gamma{H} - \gamma{L}) \left[ 1 - e^{-c\left(\frac{D(u,v)}{D0}\right)^{2}} \right] + \gamma{L}$
(1)参数选择:参考$\gamma{H}$=2,$\gamma{L}$ = 0.25 , $C$ = 1。
(2)自己尝试不同的 $D_0$ 以得到最好的结果。
(3)如将滤波器替换为一阶Butterworth高通滤波器,比较滤波结果。
提示:对于滤波输出图像, 确定图像的最大和最小像素值max和min, 得到range=max-min,
对于f(x,y),以255*(f(x,y)-min)/range,得到最好的显示效果。
首先我们将原图转为灰度图像,同时由于后续要进行对数和指数操作,所以使用im2double将图像矩阵转为双精度
1 | img = imread('office.jpg'); |
我们将图像转为对数域,获取对数域的图像尺寸,然后进行傅里叶变换
1 | imgLog = log(1 + img); |
在设置滤波器参数后,我们创建同态滤波器
1 | gammaH = 2; |
在对图像进行同态滤波后,对其进行傅里叶反变换以及指数操作
1 | G = H .* fftShift; |
最后我们需要归一化图像,使得亮度显示效果最佳
1 | % 确定最大和最小像素值 |
我们将多个不同$D_0$值得到的滤波后结果放在一起对比,找出最好的结果
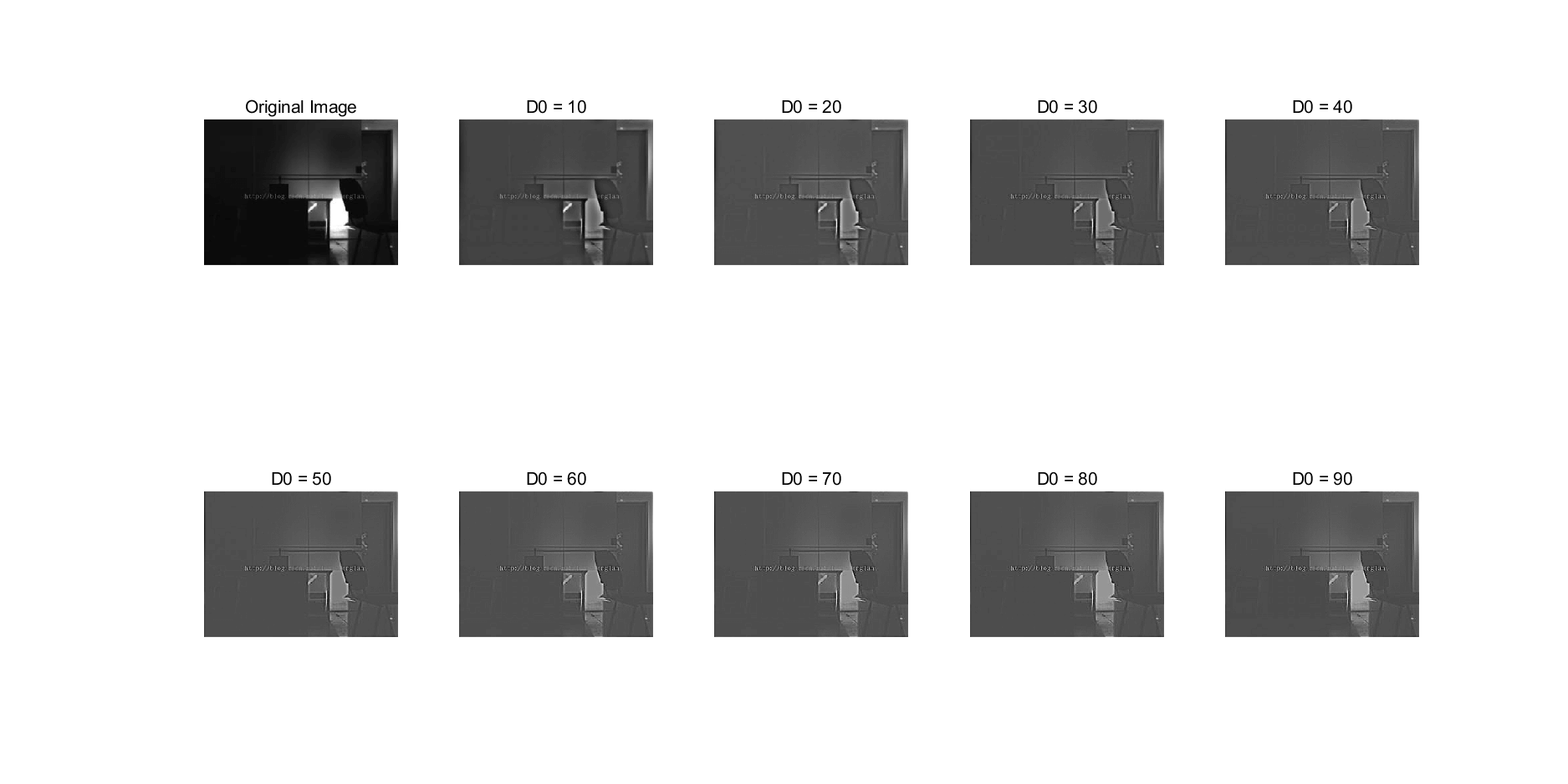
可以看出,当$D_0$为50时,效果就已经很好了
我们再创建一个1阶butterworth高通滤波器
1 | n = 1; |
展示D0=10时的对比结果

能够发现,虽然高通滤波器也能增加图像细节,但是图像的光照效果并不均匀