LSB隐写算法的基本实现

LSB隐写原理

LSB全称为 Least Significant Bit（最低有效位），是一种常被用做图片隐写的算法。LSB属于空域算法中的一种，是将信息嵌入到图像点中像素位的最低位，以保证嵌入的信息是不可见的，但是由于使用了图像不重要的像素位，算法的鲁棒性差，水印信息很容易为滤波、图像量化、几何变形的操作破坏。

图像在取样和量化后，可以存储为一个了 M 行 N 列的数字图像$I(x,y)$（二维矩阵）如下：

$I(x,y) = \begin{bmatrix} I(0,0) & I(0,1) & \cdots & I(0,N-1) \ I(1,0) & I(1,1) & \cdots & I(1,N-1) \ \vdots & \vdots & \ddots & \vdots \ I(M-1,0) & I(M-1,1) & \cdots & I(M-1,N-1) \ \end{bmatrix} $

在灰度图像中任意的 $I(x,y)$都存储了对应这一点的二进制八位的灰度值（RGB 图像则是对应的三通道彩色像素值）

要实现LSB隐写算法，首先将需要隐藏的信息转换为二进制形式。然后，遍历图像的每个像素，将信息的二进制位依次嵌入到像素值的最低位中。例如，如果要隐藏的信息是一个二进制序列1011，那么算法将取图像的前四个像素（对于灰度图像）或第一个像素的RGB三个通道加一个额外通道（对于彩色图像），并将每个像素（或通道）的最低位修改为该二进制序列的一个位。

代码实现

信息与二进制互相转换

在LSB隐写中，信息是以二进制的形式嵌入在图像中，所以无论是隐写还是从图像中提取信息，都会涉及到信息（字符串）与二进制的相互转换

首先，信息转换成二进制的功能通过message_to_bin函数实现。该函数接收一个字符串作为输入，并将每个字符转换成其ASCII编码的二进制表示，最后将这些二进制字符串连接起来形成一个长的二进制序列

1
2
3
4
5
def message_to_bin(message):
    """将消息转为二进制编码"""

    binary = ''.join([format(ord(i), "08b") for i in message])
    return binary

我们使用"08b"的形式使最后的二进制编码为8位，前面不足的位数补零

将二进制转为字符串时，我们将二进制编码先分为8位长度的块，每个块代表字符串中的一个字符，然后用chr()强转为字符

1
2
3
4
5
def bin_to_message(binary):
    """将二进制编码转为消息"""

    message = ''.join([chr(int(binary[i:i+8], 2)) for i in range(0, len(binary), 8)])
    return message

隐写

为了方便从隐写图像中提取信息，我们需要在隐写时在嵌入的信息末尾加上结束符

这里我们使用8*n_bits个1和n_bits个0作为结束符，这样嵌入的像素个数为整数，而且由于一长串的 1 后跟几个 0在正常的文本转换为二进制后的模式中很少出现，所以非常适合作为结束符

1
2
3
4
5
# 用结束符来标记消息的结束
delimiter = '1' * (n_bits * 8) + '0' * n_bits
binary_message = message_to_bin(message) + delimiter
# 将二进制编码分割为 n_bits 位的块
bit_chunks = [int(binary_message[i:i+n_bits], 2) for i in range(0, len(binary_message), n_bits)]

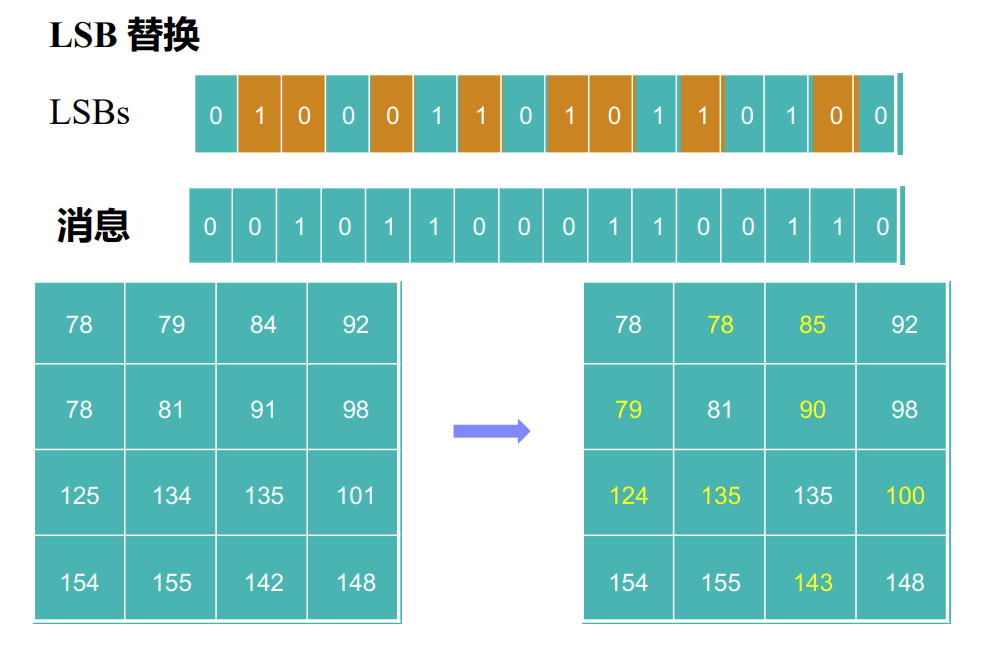
接下来我们将图像的像素值转为二进制编码，并最后 n_bits 位替换为消息的二进制编码

1
2
3
4
5
6
7
8
9
10
for index, pixel in np.ndenumerate(pixels):
    if data_index < len(bit_chunks):
        # 将原图像的像素值的最后 n_bits 位替换为消息的二进制编码
        mask = ~((1 << n_bits) - 1)
        bits = bit_chunks[data_index]
        new_pixel = (pixel & mask) | bits
        new_pixels[index] = new_pixel
        data_index += 1
    else:
        break

提取信息

当我们从灰度图像中提取隐藏的消息时，需要先将图像的每个像素值中获取后n_bits位，并将它们串起来

1
2
3
for pixel in np.nditer(pixels):
    # 确保从每个像素提取的消息为 n_bits 位
    binary_message += format(pixel & ((1 << n_bits) - 1), f'0{n_bits}b')

接下来找到消息末尾的结束符，并从该处截断消息

1
2
3
4
# 找到结束符，并从该处截断消息
delimiter = '1' * (n_bits * 8) + '0' * n_bits
delimiter_index = binary_message.find(delimiter)
binary_message = binary_message[:delimiter_index]

测试结果

测试图片我们选择使用数字图像处理领域的经典样本Lena（灰度图，256*256分辨率）

较低分辨率是为了使得测试信息更好地散布在更多比例的像素点上

原图如下

lena

首先我们向图片的最低位嵌入信息Hello, My name is R1ck. Welcome to R1ck's Portal! Can you catch the flag?

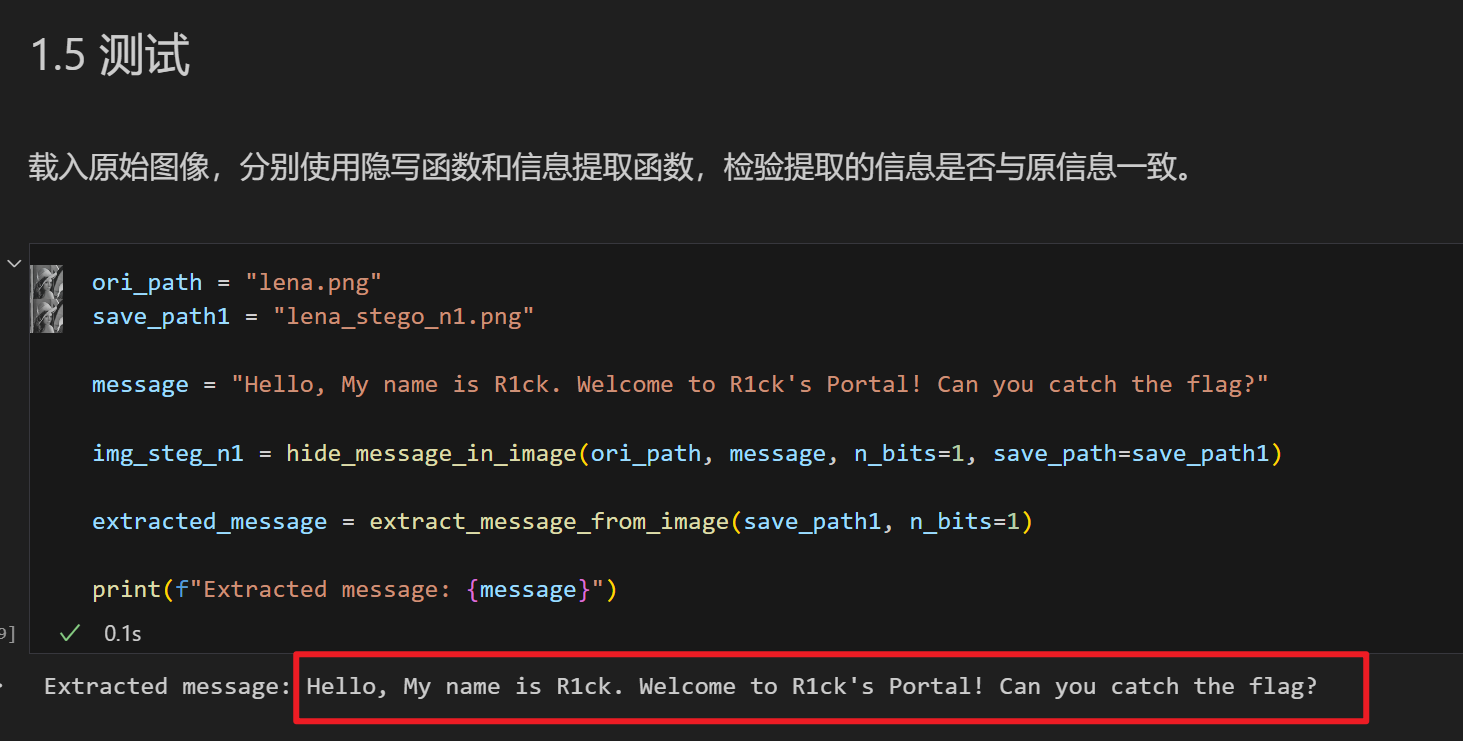
成功提取出嵌入的字符串

我们试着比较一下嵌入不同位数对隐写图像在视觉上的影响

可以发现当我们将消息嵌入在后4位以内时，图像在视觉上变化不大

用卡方分布检测进行隐写分析

卡方分布检测原理

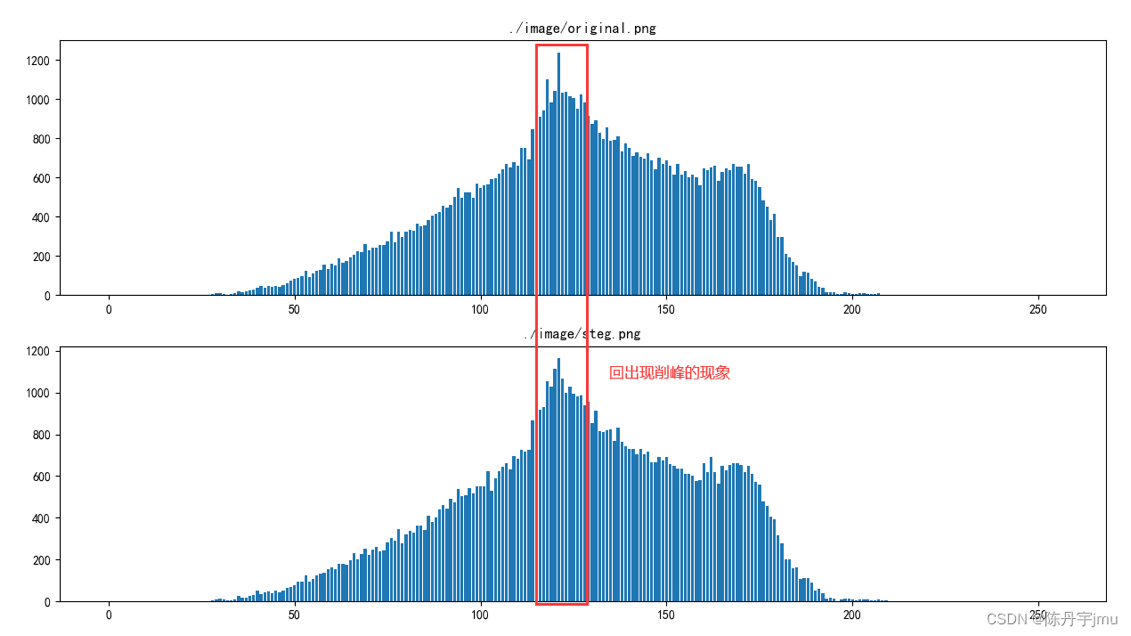
灰度直方图是关于图像灰度级分布的函数，它将数字图像中的所有像素，按照灰度值的大小，统计其出现的次数，即图像中具有某种灰度级的像素的个数。在原始图像（灰度值为0-255）中，相邻灰度值的像素块数目一般差别很大。但在 LSB 信息隐藏中，秘密信息在嵌人之前往往经过加密，可以看作是 0、1 随机分布的比特流，而且值为 0 与 1 的可能性都是1/2。如果秘密信息完全替代载体图像的最低位，那么伪装对象相邻灰度值的像素块数目将会比较接近，这个被称之为“值对效应”。我们就可以根据这个性质判断图像是否经过隐写。如下图可以看到，经过 LSB 隐写的灰度图像出现了更多的“回削峰”

卡方检验用于统计样本的实际观测值与理论推断值之间的偏离程度，实际观测值与理论推断值之间的偏离程度就决定卡方值的大小，如果卡方值越大，二者偏差程度越大；反之，二者偏差越小；若两个值完全相等时，卡方值就为 0，表明理论值完全符合。

设图像中灰度值为 j 的像素数为 h(j) , 其中 0 ≤ j ≤ 255。灰度直方图横坐标为 j ，纵坐标为 h (j) 。如果载体图像未经隐写，h(2i) 和 h(2i+1) 的值会相差得很远，如果秘密信息完全替代载体图像的最低位,那么 h(2i) 和 h(2i+1) 的值会比较接近。嵌入信息会改变灰度直方图的分布，由差别很大变得近似相等,但是却不会改变 h(2i) + h(2i+1) 的值,因为样值要么不改变，要么就在 h(2i) 和 h(2i+1) 之间改变。

比较灰度直方图

首先使用cv2库中的calcHist函数计算出原图和隐写图片的灰度直方图，并展示在一起

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
img_ori = cv2.imread(ori_path, cv2.IMREAD_GRAYSCALE)
img_steg_n1 = cv2.imread(save_path1, cv2.IMREAD_GRAYSCALE)

hist_ori = cv2.calcHist([img_ori], [0], None, [256], [0,256]).flatten()
hist_stego = cv2.calcHist([img_steg_n1], [0], None, [256], [0,256]).flatten()

fig, axs = plt.subplots(2, 1, figsize=(8, 6))

axs[0].bar(range(256), hist_ori, color='gray')
axs[0].set_title('Original Image Histogram')
axs[0].set_xlim([0, 255])

axs[1].bar(range(256), hist_stego, color='gray')
axs[1].set_title('Stego Image Histogram')
axs[1].set_xlim([0, 255])

plt.tight_layout()
plt.show()

得到的对比图像如下

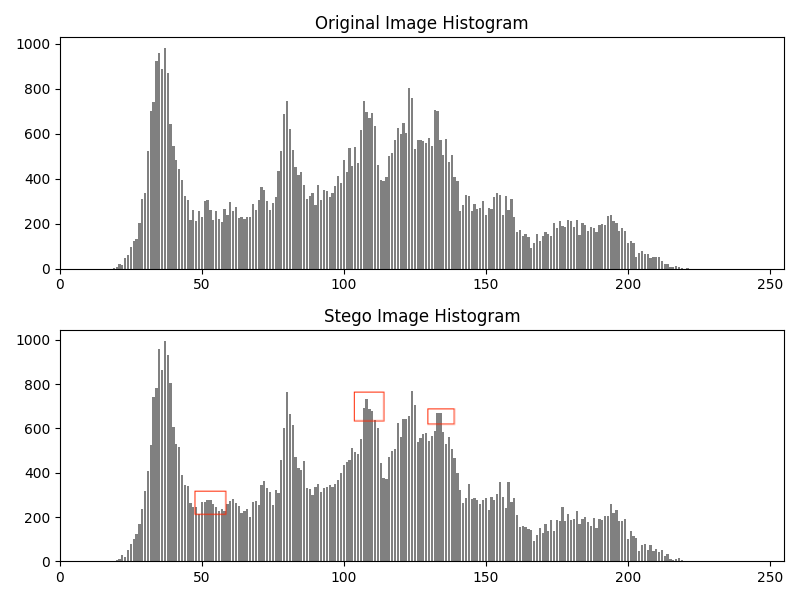
可以看到红框圈出的位置确实出现了削峰现象

计算r和p值

偏差r服从卡方分布

$ h{2i}^* = \frac{h{2i} + h{2i+1}}{2}, \quad q = \frac{h{2i} - h_{2i+1}}{2}$

$r = \sum{i=1}^{k} \left(\frac{(h{2i} - h{2i}^*)^2}{ h{2i}^*}\right)$

我们使用循环遍历灰度值对，累加卡方值

1
2
3
4
5
6
7
8
9
10
11
12
13
# 遍历灰度值对，计算卡方值
for i in range(0, 256, 2):

    if i + 1 >= 256:
        break
    # 计算每对的像素总数
    pair_total = hist[i] + hist[i + 1]
    if pair_total == 0:
        continue  # 避免除以0

    # 计算并累加卡方值
    r += ((hist[i] - hist[i + 1]) ** 2) / pair_total / 2
    k += 1

结合卡方分布的密度计算函数，我们可以计算载体被隐写的可能性p

1
p = 1 - chi2.cdf(r, k - 1)

这里使用的是scipy库中的计算卡方分布累积分布函数的方法chi2.cdf

我们分别计算原图以及上一个任务的隐写图像的r和p值

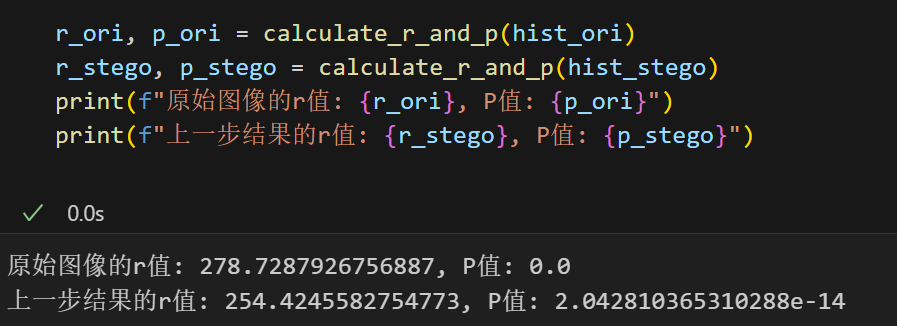
可以发现相较于原图，隐写图像的r值有所下降，说明经过载密后载体含有秘密信息的可能性变大

而可能性p值增加的不那么明显

经过分析，我认为可能有两点原因：

  1. 之前测试时在图像中嵌入的信息长度太短，嵌入率太低
  2. 嵌入的字符串转化成的二进制编码中的0和1的分布不太接近

比较不同嵌入率下r和p的变化规律

根据上一步的结论，我认为增大嵌入率后，p值能够有明显的变化

这里我们直接使用random库来生成随机的二进制编码序列

分别生成嵌入率为50%和100%的隐写图像并分析

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
pix_num = img_ori.shape[0] * img_ori.shape[1]

# 生成长度为图像分辨率1/2的随机二进制编码
binary_half = ''.join(random.choices('01', k=pix_num // 2))

# 生成长度为图像分辨率的随机二进制编码
binary_full = ''.join(random.choices('01', k=pix_num - 9))

img_steg_half_pixels , _ =hide_message_in_image(ori_path, binary=binary_half, n_bits=1)
img_steg_half = img_steg_half_pixels.reshape((img_ori.shape[0], img_ori.shape[1]))
img_steg_full_pixels , _ = hide_message_in_image(ori_path, binary=binary_full, n_bits=1)
img_steg_full = img_steg_full_pixels.reshape((img_ori.shape[0], img_ori.shape[1]))


hist_half = cv2.calcHist([img_steg_half], [0], None, [256], [0,256]).flatten()
hist_full = cv2.calcHist([img_steg_full], [0], None, [256], [0,256]).flatten()

r_half, p_half = calculate_r_and_p(hist_half)
r_full, p_full = calculate_r_and_p(hist_full)

print(f"嵌入率50%时的r值: {r_half}, P值: {p_half}")
print(f"嵌入率100%时的r值: {r_full}, P值: {p_full}")

运行结果如下

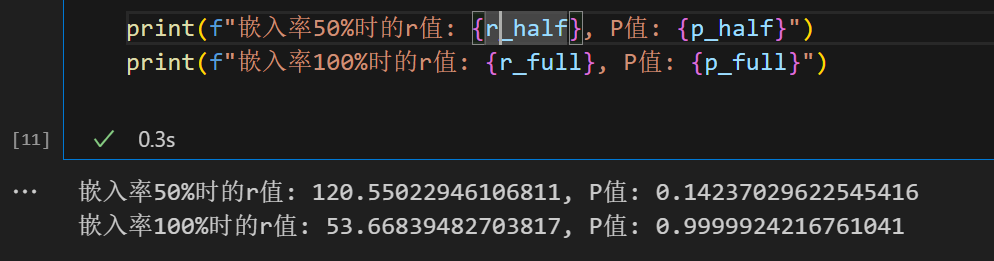
可以发现嵌入率在100%时，p值能达到99%，说明p值对嵌入的检测还是较为敏感的

嵌入的信息确实使得相邻灰度值的数量变得接近

下面我们比较一下不同嵌入率下的平均r值和p值（从0到100%，间隔2%）

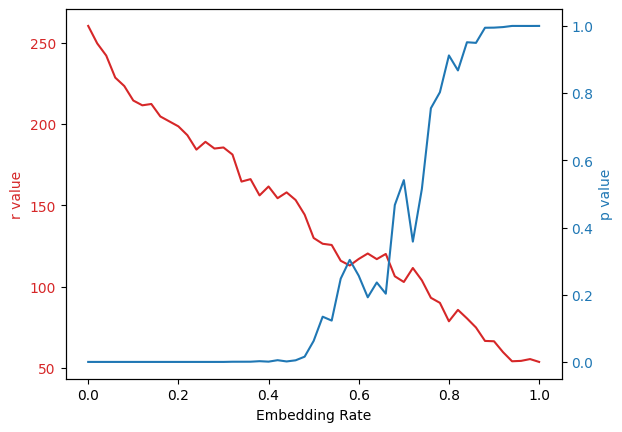
可以发现图中的曲线虽然在部分区域有震荡，但总体上r值随嵌入率的增加呈降低趋势，而p值呈上升趋势

在嵌入率到50%之前，p值上升的较为缓慢，而嵌入率到80%之后，p值稳定在95%以上

LSB 的改进

随机LSB替换

随机LSB替换将嵌入位置改为约定好的随机位置，这样可以有效降低对统计特性的影响

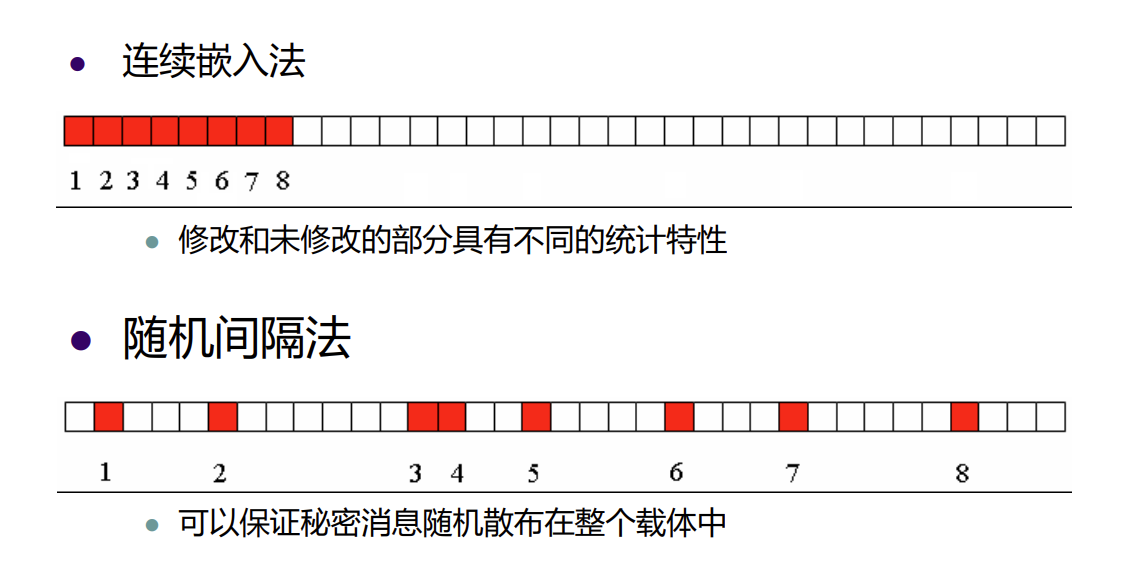
我们只需改进原来算法中的遍历像素值的部分

通过设置随机种子seed，我们可以确保提取时产生相同的随机序列

1
2
3
4
5
6
# 设置随机种子以确保过程可重复
random.seed(seed)
# 生成随机替换的像素索引
indices = list(range(len(flat_pixels)))
random.shuffle(indices)
indices = indices[:len(bit_chunks)]

使用random.shffle方法，我们可以获得一个随机的迭代器

LSBM

相比于随机LSB替换从秘密消息的散布上下手，LSBM算法则是从值对现象本身出发

如果载体图像被选定的、待嵌入的像素点的LSB 与二进制形式的秘密信息不同，则对该 LSB 任意地+1 或者-1，以

防止攻击者的“值对”分析

这里我们只需改进原版LSB算法修改像素点的部分

当待嵌入的像素点的LSB 与二进制形式的秘密信息不同时，使用random.randint函数选择加一或减一操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
for data_index, bit in enumerate(bit_chunks):
    pixel_value = new_pixels[data_index]
    bit_to_hide = int(bit, 2)

    if pixel_value % 2 != bit_to_hide:
        if random.randint(0, 1) == 1:
            # 确保加1后不超过255
            if pixel_value < 255:
                new_pixels[data_index] += 1
            else:
                new_pixels[data_index] -= 1
        else:
            # 确保减1后不小于0
            if pixel_value > 0:
                new_pixels[data_index] -= 1
            else:
                new_pixels[data_index] += 1

测试

首先我们测试一下这两种改进算法能否嵌入信息以及提取信息

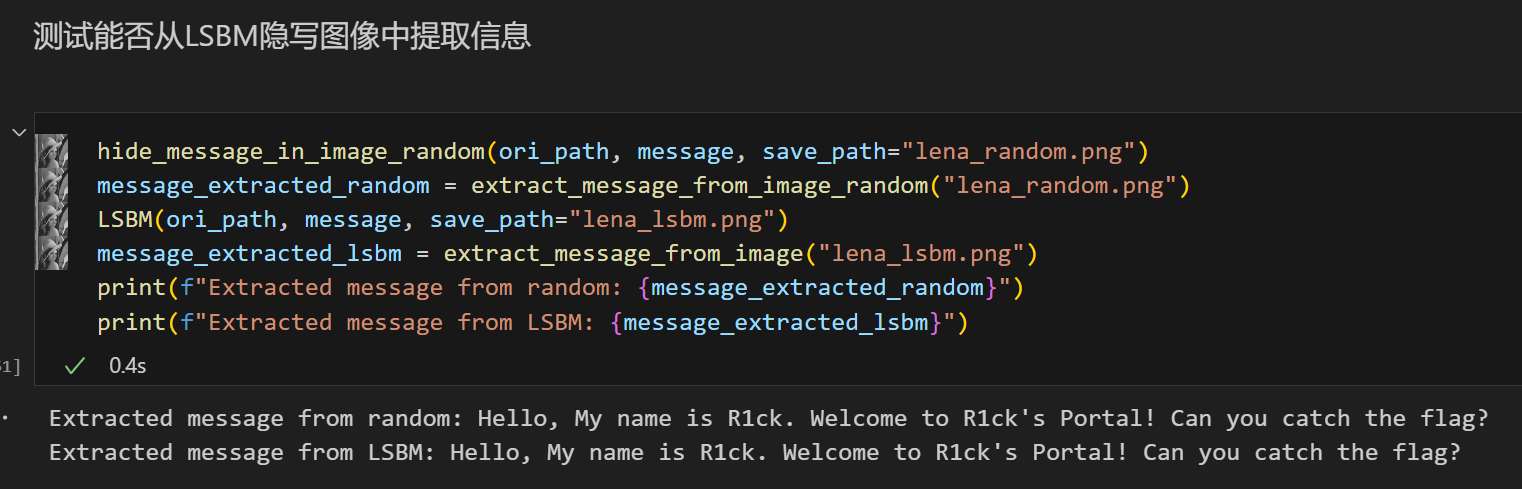
算法实现成功

接下来我们使用隐写分析比较普通LSB算法、随机LSB替换算法和LSBM算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
img_steg_lsb_random , _ =hide_message_in_image_random(ori_path, binary=binary_full)
img_steg_lsb_random = img_steg_lsb_random.reshape((img_ori.shape[0], img_ori.shape[1]))
img_steg_lsbm , _ = LSBM(ori_path, binary=binary_full)
img_steg_lsbm = img_steg_lsbm.reshape((img_ori.shape[0], img_ori.shape[1]))


hist_random = cv2.calcHist([img_steg_lsb_random], [0], None, [256], [0,256]).flatten()
hist_lsbm = cv2.calcHist([img_steg_lsbm], [0], None, [256], [0,256]).flatten()

r_random, p_random = calculate_r_and_p(hist_random )
r_lsbm, p_lsbm = calculate_r_and_p(hist_lsbm )

print(f"普通LSB算法的r值: {r_full}, P值: {p_full}")
print(f"随机LSB替换算法的r值: {r_random}, P值: {p_random}")
print(f"LSBM算法的r值: {r_lsbm}, P值: {p_lsbm}")

运行结果如下

可以看到，相较于普通LSB算法的r值，两种改进算法都有提高

而两种改进算法的p值也成功降低，说明这两种改进方法都能在一定程度上对抗隐写分析

相较而言，LSBM算法的效果要比随机LSB替换算法更好